Electromagnetic Emission From Hot Medium Measured by the PHENIX Experiment at RHIC
November 17, 2011

Takao Sakaguchi is a physicist at Brookhaven working on the PHENIX experiment. This article is based on a talk he gave at the Rutherford Centennial Conference in Manchester, celebrating Rutherford's discover of the nucleus 100 years ago.
By Takao Sakaguchi
Abstract
Electromagnetic radiation has been of interest in heavy ion collisions because they shed light on early stages of the collisions where hadronic probes do not provide direct information since hadronization and hadronic interactions occur later. The latest results on photon measurement from the PHENIX experiment at RHIC reflect thermodynamic properties of the matter produced in the heavy ion collisions. An unexpectedly large positive elliptic flow measured for direct photons is difficult to explain in any of the current models.
Introduction
Many intriguing phenomena have been observed at RHIC since it started of running in 2000. The high transverse momentum (pT) hadron production from the initial hard scattering was observed, and the large suppression of their yields suggested that the matter is sufficiently dense to cause parton-energy loss prior to hadronization [1]. The large elliptic flow of particles and its scaling in terms of particle kinetic energy suggests that the system is locally in equilibrium as early as 0.3 fm/c, and the flow occurs already on the partonic level.
Because they interact with the medium and other particles only electromagnetically and are largely unaffected by final state interactions, photons serve as a direct and penetrating probe of the early stages at high temperature and high density [2]. At leading order, the production processes of photons are annihilation (qq→γg) and Compton scattering (qg → γq) (Figure 1). Their yields are proportional to ααs, which are  ∼ 40 times lower than hadrons from strong interactions.
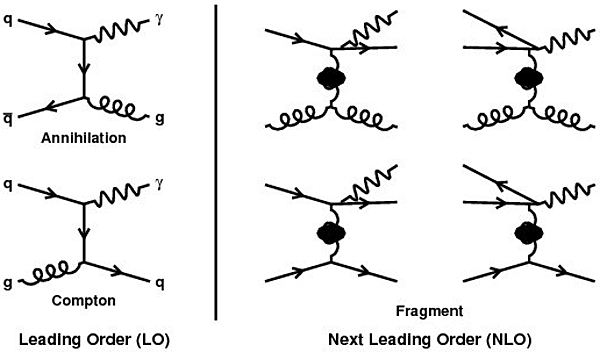
Figure 1: Photon production process.
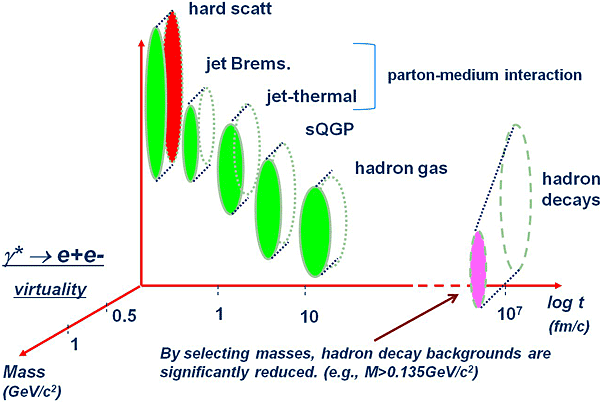
Figure 2: Sources of photons from various stages of collisions.
A calculation predicts that the photon contribution from the QGP state is predominant in the pT range of 1 < pT < 3 GeV/c [3]. For pT > 3 GeV/c, the signal is dominated by a contribution from initial hard scattering, and pT < 1 GeV, the signal is from hadron gas through processes of ππ(ρ) → γρ(π), πK* → K γ and etc. Figure 2 shows a landscape of photon sources as a function of the time they are produced. The vertical axis corresponds to transverse momenta of photons. We have one another degree of freedom, virtual mass, in photon measurement, which will be explained in detail in a later section. These photons can be measured after a huge amount of background photons coming from hadron decays (π0, η, η′ and ω, etc.) are subtracted off from inclusive photon distributions. The typical signal to background ratio is  ∼ 1 % at 2 GeV, and  ∼ 10 % at 5 GeV in case of p+p collisions. The signal from QGP is predicted to be  ∼ 10 % of the inclusive photons. For Au+Au collisions, thanks to a large suppression of high pT hadrons, the ratio is enhanced by the same degree.
Measurement of initial hard scattering photons in heavy ion collisions
One of the big successes by now in electro-magnetic radiation measurements is the observation of high pT direct photons that are produced in initial hard scattering [5] in relativistic heavy ion collisions. Figure 3 shows the direct photon spectra in Au+Au collisions at √{sNN}=200 GeV for different centralities.
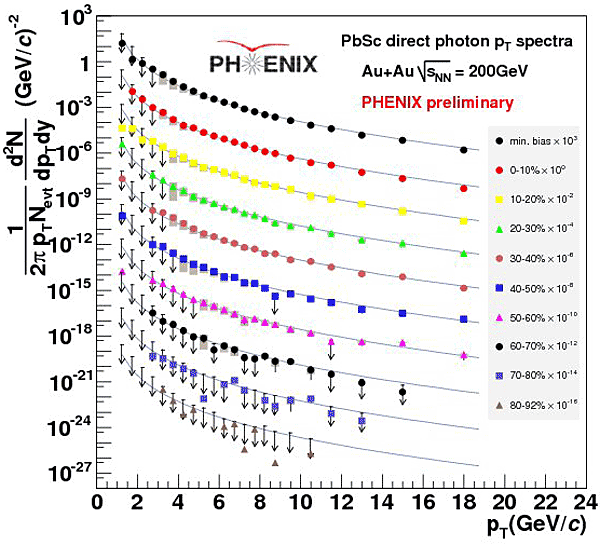
Figure 3: Direct photon spectra in Au+Au collisions at √{sNN}=200 GeV.
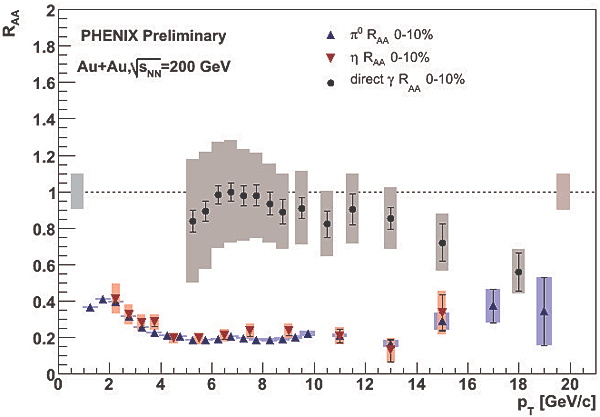
Figure 4: Nuclear modification factors (RAA for photons, π0 and η in 10 % central Au+Au collisions at √{sNN}=200 GeV.
The lines show the NLO pQCD calculations [6] scaled by the nuclear thickness function (TAA). The fact that the data are well described by the lines show that the yields are following the TAA scaling and suggest that the source is the initial hard scattering. Figure 4 shows the nuclear modification factors (RAA) for direct photons, π0 and η for 0-10 % central Au+Au collisions at the same center-of-mass (cms) energy. RAA is defined as the ratio of the yield in nucleus-nucleus collisions divided by that in p+p collisions scaled by TAA. The high pT hadron suppression is interpreted as a consequence of an energy loss of hard-scattered partons in the hot and dense medium. It was strongly supported by the fact that the high pT direct photons are not suppressed and well described by a NLO pQCD calculation. The small suppression seen in the highest pT is likely due to the fact that the ratio of the yields in Au+Au to p+p was computed without taking the isospin dependence of direct photon yields into account [7].
Measurement of direct photons through its internal conversion
There is a huge background arising from π0 decaying into two photons, which makes it very difficult to look at the direct photon signal at low pT, where thermal photons from QGP manifest, with traditional calorimetry of (real) photons. However, if we look at photons with a small mass (virtual photons) instead, we can select the mass region where π0 contribution ceases (Fig 5). For the case of pT >> M, the yield of virtual photons is expected to be dominated by internal conversion of real photons [8,9]. For obtaining direct photon yield, we fit the measured invariant mass distribution with the function:
|
where fc is the cocktail calculation (photons from various hadron decays), fd is the mass distribution for direct photons, and r is the free parameter in the fit. Next, using the Kroll-Wada formula [10] to account for the Dalitz decays of π0, η and direct photons, r is defined as the ratio of direct photons to inclusive photons:
|
Then, the invariant yield of direct photons is calculated as γinc ×rγ. As described in [9], the procedure is demonstrated in Fig 5 for 1.0 < pT < 1.5 GeV/c.
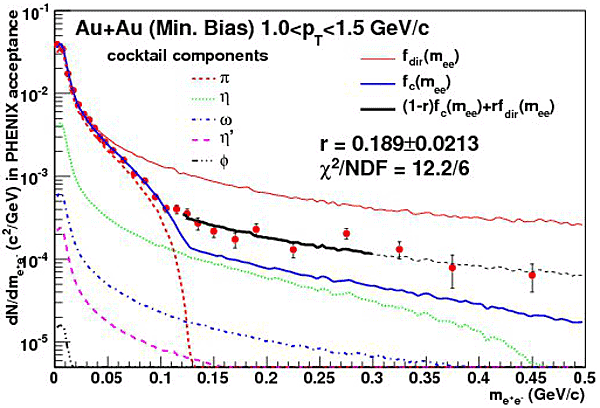
Figure 5: Invariant mass distributions of electron-pairs and comparison with possible hadron sources of electron-pairs.
The dotted lines show the contributions from various hadrons, the solid blue is the sum of these contributions, and the solid red line shows the distribution from direct photons converted internally. The r value is determined by the fit to the data. The error of the fit corresponds to the statistical error. We applied the procedure as a function of pT for various centrality selections in p+p and Au+Au collisions, and obtained the pT spectra, as shown in Fig 6.
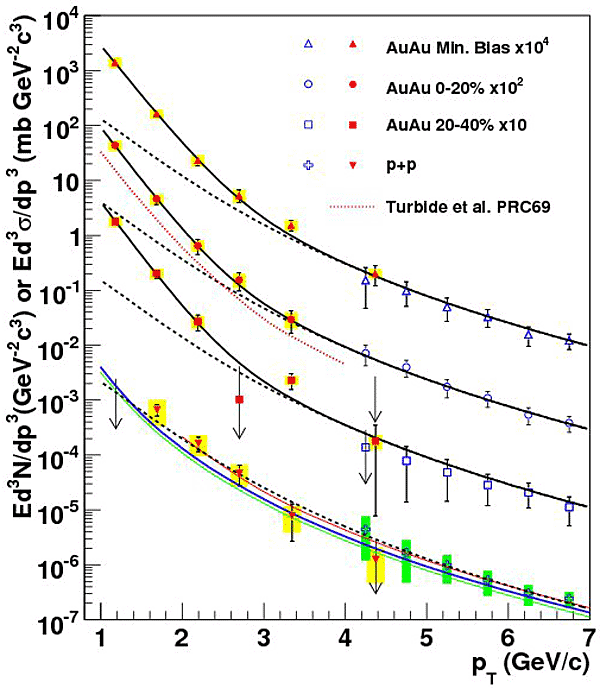
Figure 6: Direct photon spectra obtained from the measurement of internal conversion of photons in Au+Au collisions.
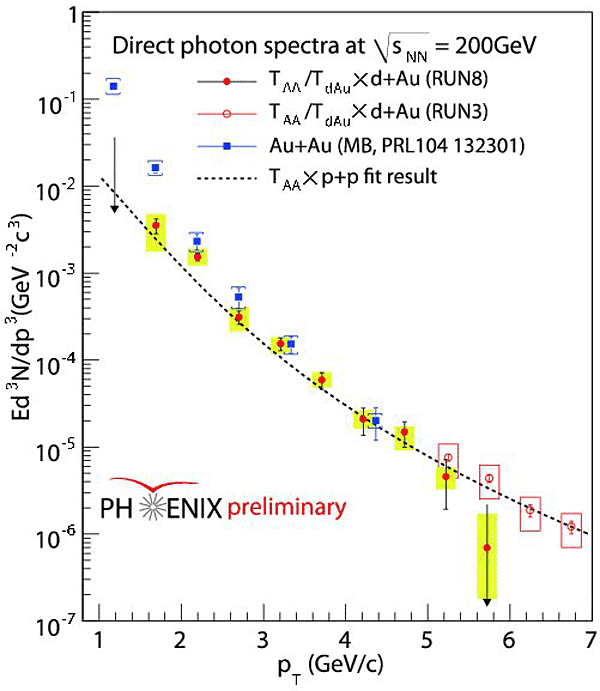
Figure 7: Direct photon yield in Au+Au and d+Au collisions scaled by the difference of Ncoll.
The distributions are for 0-20 %, 20-40 % centrality and MB events for Au+Au collisions. For pT < 2.5 GeV/c the Au+Au yields are visibly higher than the scaled p+p yield. The distributions were then fitted with the p+p fit plus exponential function to obtain slopes and dN/dy for three centralities. The slopes are estimated to be  ∼ 220 MeV. The lines show the theoretical expectation from a literature [3]. One may question whether or not the excess arises from a source that exists only in Au+Au collisions. For example, an effect that could increase the yield is cold-nuclear-matter (CNM) effect such as kT broadening (Cronin effect). To quantify the contribution we analyzed 2008 d+Au data with the same procedure [11]. Figure 7 shows the Au+Au yield compared to the d+Au yield scaled by Ncoll. It clearly shows that there is an enhancement over CNM effects in Au+Au collisions.
Exploring new degree of freedom in direct photon measurement
On exploring the matter produced, one wants to explore a new degree of freedom of the observables. The angular dependence of the photon yield with respect to the plane defined by impact parameter (event plane) is one of the degrees that can be investigated. Rapidity dependence will be another degree of freedom, which may shed light to the pre-equilibrium state of the collisions.
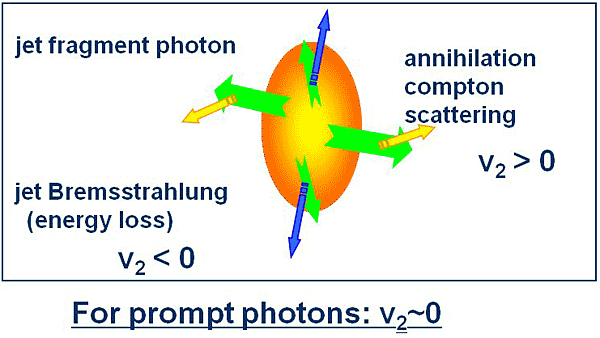
Figure 8: Source dependence of elliptic flow (v2) of direct photons.
It is predicted that the elliptic flow of photons show the different sign and/or magnitude, depending on the production processes [12] (Fig. 8). The observable is powerful to disentangle the contributions from various photon sources in the pT region where they intermix. The photons from hadron-gas interaction and thermal radiation may follow the collective expansion of a system, and give a positive v2. The amount of photons produced by jet-photon conversion or in-medium bremsstrahlung increases as the medium to traverse increases. Therefore these photons show a negative v2. The fragmentation photons will give positive v2 since larger energy loss of jets is expected orthogonal to the event plane.
PHENIX has measured the v2 of direct photons by subtracting the v2 of hadron decay photons off from that of the inclusive photons, following the formula below:
|
The elliptic flow of π0 and inclusive photons are shown in Fig. 9(a), and the one for direct photons is shown in Fig. 9(b).
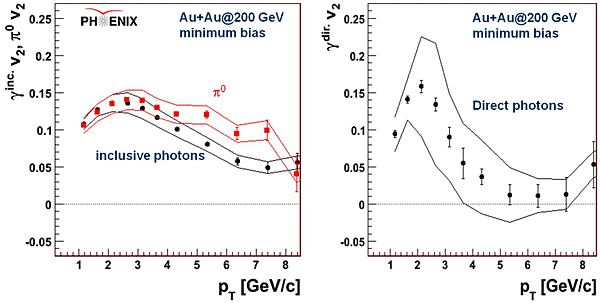
Figure 9: Elliptic flow of (a, left) π0 and inclusive photons and (b, right) direct photons.
The v2 of direct photons is large and positive, and comparable to the flow of hadrons for pT < 3 GeV/c. This result is hard to explain by many models. Several models qualitatively predicted the positive flow of the photons assuming the photons are boosted with hydrodynamic expansion of the system, but the amount is significantly lower than the measurement [13]. There is one model that gives relatively large flow by including the hadron-gas interaction [14].
Summary
Direct photons are a powerful tool to investigate the collision dynamics. PHENIX has measured direct photons over wide pT ranges, including hard scattering and thermal photons, and extracted quantities, such as slope parameters, that reflect thermodynamic properties of the matter. An unexpectedly large positive elliptic measured for direct photons is difficult to explain by many models.
References
[1]
K. Adcox, et al. (PHENIX Collaboration), Nucl. Phys. A757 (2005) 184-283.
[2]
P. Stankus, Ann. Rev. Nucl. Part. Sci. 55 (2005) 517-554.
[3]
S. Turbide, R. Rapp, C. Gale, Phys. Rev. C 69 (2004) 014903.
[4]
K. Adcox, et al., Nucl. Instrum. Meth. A499 (2003) 469-479.
[5]
S. S. Adler et al. (PHENIX Collaboration), Phys. Rev. Lett. 94, 232301 (2005).
[6]
L. E. Gordon, W. Vogelsang, Phys. Rev. D 48 (1993) 3136-3159.
[7]
F. Arleo, JHEP 0609, 015 (2006).
[8]
A. Adare, et al. (PHENIX Collaboration), Phys. Rev. Lett. 104 (2010) 132301.
[9]
A. Adare, et al. (PHENIX Collaboration), Phys. Rev. C 81 (2010) 034911.
[10]
N. M. Kroll, W. Wada, Phys. Rev. 98 (1955) 1355-1359.
[11]
T. Sakaguchi, Nucl. Phys. A855, 141-148 (2011).
[12]
S. Turbide, C, Gale and R.J. Fries, Phys. Rev. Lett. 96, 032303 (2006); R. Chatterjee et al., Phys. Rev. Lett. 96, 202302 (2006)
[13]
R. Chatterjee, D. Srivastava, Phys. Rev. C 79 (2009) 021901.
[14]
H. van Hees, C. Gale and R. Rapp, arXiv:1108.2131.
2011-2724 | INT/EXT | Newsroom