Research
Petascale Parallel Computing with ComCTQMC
Impurity models lie at the heart of electronic structure calculations using dynamical mean-field theory (DMFT). Continuous-time quantum Monte Carlo (CTQMC) is a stochastic algorithm for solving impurity models. CTQMC expands the impurity model’s partition function as a power series in the hybridization between the impurity and the bath, and then samples this power series using a Markov chain Monte Carlo algorithm. Each term in the power series is a Markov chain, and is evaluated by multiplying many matrices by each other. One of the chief computational difficulties with CTQMC is the size and number of these matrices, which strongly depends on the impurity problem. In particular, the matrices become prohibitively large when calculating f-shell impurity models.; They also become too large when using cluster DMFT, even for small cluster sizes. This is a severe difficulty for DMFT calculations of plutonium-based compounds, cuprate superconductors, and many other important materials. An additional problem is the computation of two-particle observables. They can be prohibitively expensive, even in simple one-band models. Here we briefly describe how ComCTQMC’s parallelization strategy and algorithms overcome both of these obstacles.
ComCTQMC is parallelized to take maximum advantage of modern supercomputers containing thousands of nodes. On leadership class facilities, each node will typically contain on the order of 10 CPU's (central processing units) and 1 GPU (graphics processing unit). In order to simulate new materials and access new physical regimes, ComCTQMC must efficiently use both CPU’s and GPU’s and distribute its computational load across many nodes.
ComCTQMC scales ideally with the number of nodes and CPU's. This is easily accomplished by having each CPU generate and update its own independent Markov chain. At the end of the simulation, the results are averaged across each Markov chain. Since only Markov chain initialization and finalization require communication between CPU’s, ComCTQMC is able to divide its work efficiently between any number of them. ComCTQMC implements many algorithmic improvements [1,2] to the basic CTQMC algorithm [3], allowing it to efficiently use both CPU’s and GPU’s.
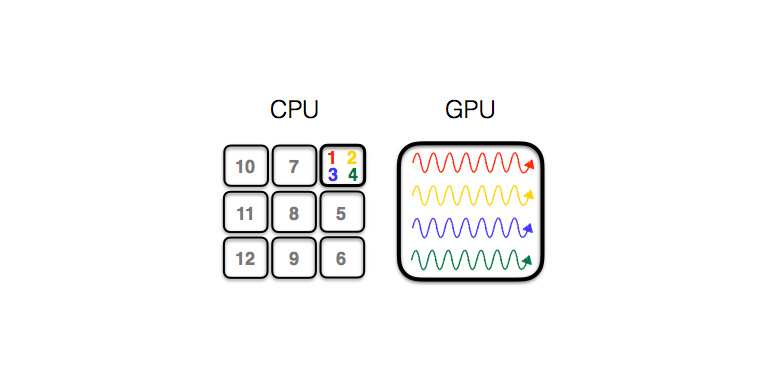
Cartoon of GPU acceleration of a CTQMC simulation: one CPU handles multiple Markov chains (1 to 4) on the GPU, the other CPU's calculate single Markov chains (5 to 12).
Making efficient use of GPU's is much more challenging than utilizing CPU's. Matrix multiplication is ComCTQMC’s dominant computational burden, and the matrices that it multiplies are relatively small compared the capabilities of a modern GPU. Therefore, multiplying the matrices in a single Markov chain will not utilize the full capabilities of a GPU. Moreover, a single GPU cannot be shared among several CPU's without either running out of memory or drastically reducing performance [2]. ComCTQMC overcomes this difficulty by pairing CPU's and GPU's. The non-paired CPU's each control a single Markov chain, as described previously, and do not use the GPU's. In contrast, the paired CPU's each control many Markov chains and delegate their matrix multiplications to the GPU. Since the GPUs each have several Markov chains to compute, their full computational power is used. ComCTQMC’s use of this parallelization scheme accelerates its calculations by a factor of 5 to 10 on the Institutional Cluster at Brookhaven National Laboratory, which has 1 GPU per node. ComCTQMC has also been run on the Summit supercomputer at Oak Ridge National Laboratory, which has 4 GPU’s per node. When calculating elemental plutonium it accelerates by a factor of 10 to 200, depending on whether crystal field effects are included in the interaction tensor.
ComCTQMC’s parallelization strategy enables it to efficiently utilize all available resources on a supercomputer; it adjusts the number of Markov chains to match the number of CPU’s and GPU’s. However, calculation of two-particle observables presents an additional daunting obstacle. This would involve sampling each Markov chain after every n steps, and would in most cases bring a CTQMC calculation to a stand-still. One option would be to calculate two-particles observables using GPUs, since the sampling method is embarrassingly parallel. Even if this strategy were adopted, standard CTQMC algorithms are very restricted; they are unable to sample many two-particle observables [4]. ComCTQMC adopts instead the worm algorithm with improved estimators [4,5], which does not share the same restriction. It allows efficient calculation of all two-particle observables, and its added computational burden is negligible.
ComCTQMC is well positioned for use in exascale high-performance computing environments. It makes efficient use of GPU’s, it exhibits ideal scaling across nodes, and it is able to efficiently measure two-particle observables. Indeed, ComCTQMC’s acceleration when calculating the electronic structure of plutonium on the Summit supercomputer’s led to an INCITE award [5]. Its worm algorithm implementation led to an ALCC award for calculating superconductivity in the unconventional superconductor LaNiO2 [6]. Both of these efforts were petascale calculations. ComCTQMC made efficient use of 1000 machine nodes in one case, and in the other all 4000 nodes in Summit; the entire supercomputer.
Related Publications
- Accelerated impurity solver for DMFT and its extensions
C. Melnick, P. Sémon, Y. Kwangmin, N. D’Imperio, A.-M. Tremblay, and G. Kotliar,
Comm. Phys. Comm. 267, 108075 (2021) - Continuous-time Monte Carlo methods for quantum impurity models
Gull, A.J. Millis, A.I. Lichtenstein, A.N. Rubtsov, M. Troyer, and P. Werner,
Rev. Mod. Phys. 83, 349 (2011) - Continuous-time quantum Monte Carlo using worm sampling
Gunacker, M. Wallerberger, E. Gull, A. Hausoel, G. Sangiovanni, and K. Held,
Phys. Rev. B 92, 155102(2015) - Worm-improved estimators in continuous-time quantum Monte Carlo
Gunacker, M. Wallerberger, T. Ribic, A. Hausoel, G. Sangiovanni, and K. Held,
Phys. Rev. B 94, 125153 (2016) - Thermal contraction and the volume explosion in elemental plutonium
Phys. Rev. Letters, C. Melnick, R. Adler, and G. Kotliar, in preparation (2021) - Response functions and superconductivity in LaNiO2, Phys. Rev. Letters
C. Melnick, R. Adler, and G. Kotliar, in preparation (2021)








