Applied Mathematics Group

Optimal Experimental Design for Cancer Drug Development

Note: this is a project under the Amalie Emmy Noether Fellowship in Applied Mathematics and Scientific Computing.

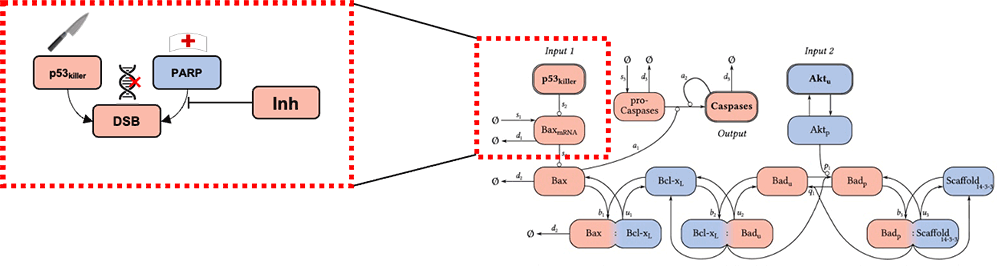
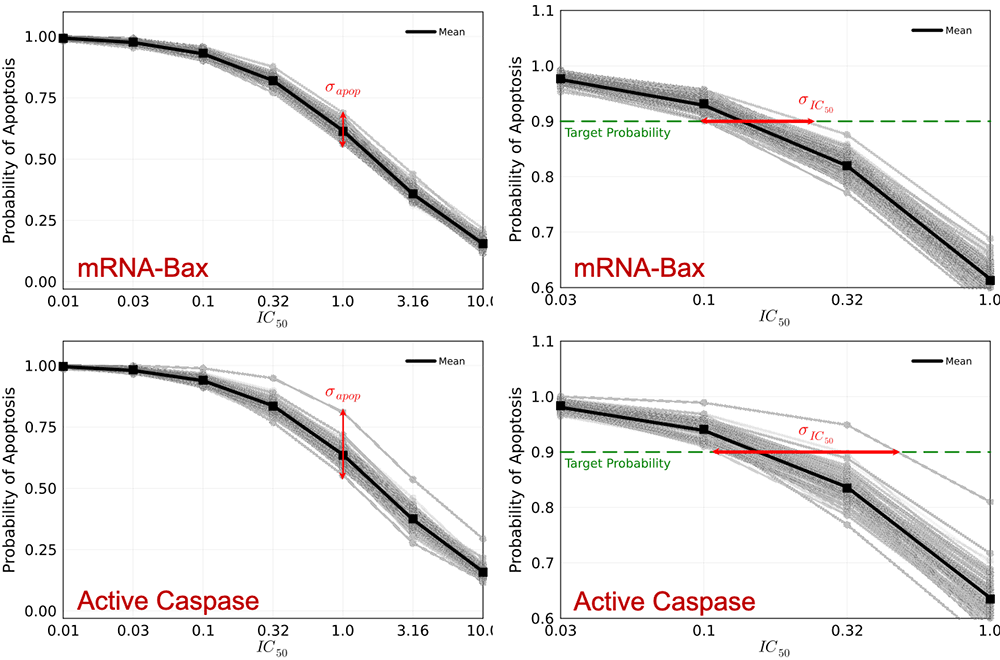
Pharmaceutical development is being impacted by generative molecular design (GMD), an artificial intelligence (AI) approach to computationally propose very large numbers of druglike molecules and adaptively screen them for desired therapeutic properties. Brookhaven, in collaboration with Frederick National Laboratory for Cancer Research and under the auspices of the Accelerating Therapeutic Opportunities in Medicine (ATOM) consortium, is examining the role of uncertainty in GMD computational pipelines. We are exploring systems biology pathway models of cellular protein-protein interactions to assess the probability that a given drug candidate will kill a cancer cell through the application of Bayesian parameter estimation in systems of ordinary differential equations. Furthermore, we are conducting Bayesian optimal experimental design to prioritize experimental measurements that will maximally reduce uncertainty in either the drug efficacy at a given level of potency or the minimum potency needed to achieve a target efficacy.

One application of scientific machine learning is to construct neural networks that emulate the behavior of physical systems, either entire computer simulations or model “parameterizations” (representations of unresolved or approximated physical dynamics). These neural network emulators then can be used to speed up calculations, assimilate information from data sources that are not present in the original model, or quantify uncertainties. Traditional deep learning methods require large amounts of simulation data to produce accurate emulators, which may not be possible to produce with limited computational budgets. We are exploring data augmentation methods that generate synthetic states for a model to simulate that are more sample-efficient in training machine learning methods.