Computer Science and Mathematics Projects
Mesoscale Models for Brittle Fracture of Solids
Mathematical models and numerical simulations of brittle fracture have attracted large attention of applied mathematicians and engineers and reached a high level of sophistication. Numerous continuum, statistical, and direct numerical simulation approaches have succeeded in the description of various features of the brittle fracture process. Despite this progress, current numerical models have limited effect on practical engineering design relevant to the DoD mission. The goal of our work is the development of a high-fidelity, high-performance finite element code with accurate models for brittle fracture. The research is based on our previously developed model that uses a mass conservative brittle fracture algorithm and scalable parallel software. In this approach, the deformation of solids was obtained via the energy minimization of elastic networks, and a conservative element-splitting algorithm was applied to overstressed elements that initiates and propagates cracks. The application of this algorithm to fundamental and engineering problems has led to numerous improvements of the description of underlying physics and numerical performance. The corresponding 3D algorithm was also developed to some, albeit lesser, extent. Unfortunately, the applicability of our brittle fracture method was limited by its compatibility with established engineering codes for solid dynamics, which are primarily based on finite element methods.
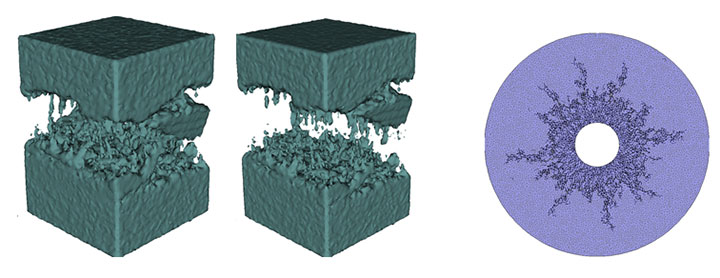
Simulation of brittle fracture of structures under external impacts.
In our current ARO-supported project, we are focusing on the adaptation of the brittle fracture method to the finite element framework in 2D and 3D, thus extending capabilities of finite element methods for the description of fracture dynamics. While the core of our new method is still based on energy minimization, our new code is based on a simplified version of the ALE (Arbitrary Lagrangian Eulerian) formulation to allow large displacement and arbitrary mesh motion, coupled with a weighted least squares formulation to calculate nodal strains and mesh adaptivity to improve accuracy and stability. The adoption of the finite element method allows the new software to be interoperable with standard FEM codes widely used for material studies, and the new approach also improves the accuracy of simulation of real materials.
Recent Publications
R. Samulyak, H. Wei, X. Jiao, T. Delaney, W. Li, C. Lu, Conservative models and numerical algorithms for brittle fracture, Technical report submitted to Army Research Laboratory, May 2014.
H. Wei, R. Samulyak, Mass-conservative network model for brittle fracture, J. Coupled Syst. Multiscale Dyn., Vol. 2 (2014), No 2, p. 2330.




