The g-2 Experiment at Brookhaven Lab
February 5, 2001

The content of this page was originally published in February 2001 when physicists announced the first results from Brookhaven Lab’s muon g-2 experiment.
A blind study
The g-2 value is actually a ratio developed by comparing two different sets of data. To minimize any possible human bias or error in this extraordinarily precise measurement, the two data sets were analyzed by separate groups of researchers, who each deliberately included artificial offsets in their result to conceal the true value and prevent unconscious bias from intruding during the analysis process. The offsets were not removed until each group was certain of the precision and accuracy of its own analysis.
A total of 68 researchers
The g-2 collaborators hail from Boston University; Brookhaven National Laboratory; Budker Institute of Technology, Novosibirsk, Russia; Cornell University; Fairfield University; Heidelberg University, Germany; KEK Laboratory, Japan; RIKEN/BNL Research Center; Tokyo Institute of Technology, Japan; University of Illinois at Urbana-Champaign; University of Minnesota; and Yale University. Full list of collaborators from these institutions.
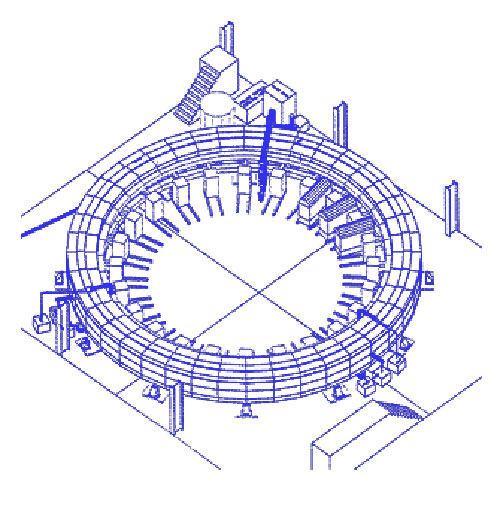
Schematic of Brookhaven's muon storage ring.
Precision analysis of huge volumes of data
The scientists collected data from more than 1 billion muon decay events. The new measurement is a factor of 5.6 more precise than previous measurements made during the 1970s at CERN, the European laboratory for particle physics near Geneva, Switzerland.
Where? The experiment takes place at the U.S. Department of Energyis Brookhaven National Laboratory, using the Alternating Gradient Synchrotron (AGS) to deliver a custom muon beam into the world's largest superconducting magnet — the "muon storage ring." The AGS provides the world's most intense multi-GeV proton beam.
What? A 1.3 parts per million (ppm) precision measurement was made of the muon's spin anomaly, termed g-2, or the "muon g-factor." The result is numerically greater than the prediction from the Standard Model theory of particle physics. The significance of the deviation is 2.6 standard deviations following standard statistical analysis. This means that there is a 99 percent probability that the measurement does not agree with the Standard Model.
Why? The muon g-factor differs from the simple prediction of g=2 by a small amount, essentially one part in 800. This tiny difference is due to the muon's interactions with virtual fields. The Heisenberg uncertainty principle permits the muon to emit and reabsorb photons, electrons, positrons, and even heavier particles such as the W and Z bosons, all of which can affect the g-factor. The electromagnetic, weak, and strong interactions all contribute to the muon anomaly. Their combined effect is calculated in the Standard Model to a precision of 0.6 ppm.
A remarkable fact is that the muon g-factor can not only be predicted to high precision, but also measured to equally high precision. Thus, a comparison of measurement and theory provides a sensitive test of the Standard Model. If there is physics not included in the current theory, and such new physics is of a nature that will affect the muon's spin, then the measurement at Brookhaven Lab would differ from the theory. This is what appears to have been observed, although there are several interpretations of the result (see below) which must be considered.
How? The measurement is enabled by four important elements:
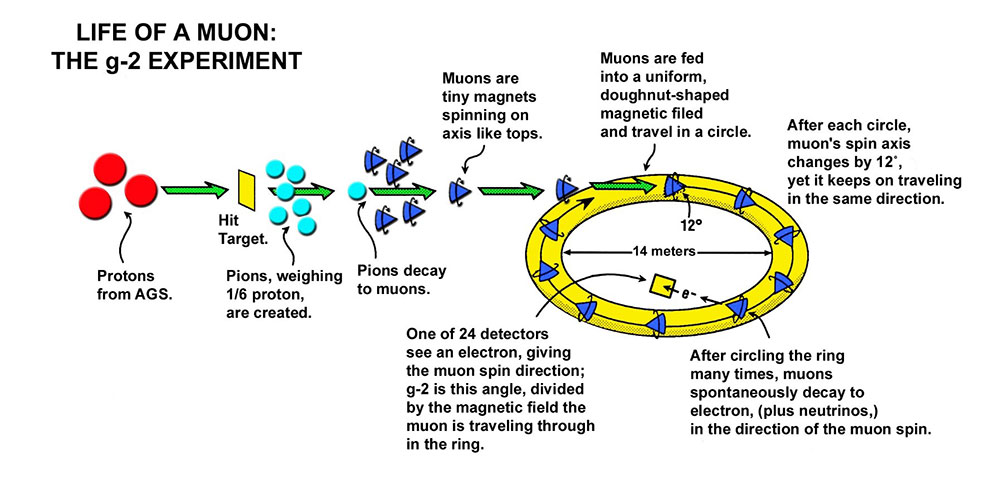
- Polarized muons (muons with their spins aligned in one direction) are injected into a storage ring whose highly uniform magnetic field is perpendicular to the muon spin direction. High-precision nuclear magnetic resonance (NMR) probes measure the strength of the magnetic field. The muons race around the ring, just like cars going around a racetrack.
- As the muon circulates around the ring, its spin, which was initially lined up in the direction of the muon motion, turns a bit faster than the muon does, so that after about 29 laps around the ring, the spin has rotated one extra time compared to the muon. The difference between the rate at which the muon itself turns around (once per lap of the ring) and the rate at which its spin rotates (called the precession), is directly proportional to the difference of the g-factor from 2. Measuring g-2 directly greatly enhances the precesion with which we can measure g. This is the key idea of measurement.
- So that the muons don't spiral up or down and out of the ring, an electric field is used to confine them. The electric field could also affect the spin, except at a "magic" speed where the electric field effect vanishes. This interaction of the muon spin and the electric field is a specific consequence of Einstein's special theory of relativity. The experiment is performed with muons at this magic speed, namely 99.94 percent the speed of light.
- To follow the precession of the muon spin, a measurement is required. Each muon is unstable (half have decayed after about 300 revolutions of the ring). When they decay, a positron (a positively charged electron, the anti-particle to the electron) is emitted whose energy carries, on average, information about the instantaneous direction of the muon spin at the time of the decay. A detector system measures the time and energy of these positrons and thus produces the experimental data of events versus time. The data look like any ordinary exponential (radioactive decay) with a modulation (wiggle) superimposed due to the muon g-factor.
Three valid ways to interpret the finding: (1) The Standard Model theory is right and requires no "new physics" and the experiment is right. There is approximately one chance in a hundred that the experimenters would find a deviation as large as reported which is simply a statistical fluctuation. The E821 (g-2) team has already obtained an additional body of similar data, having four times as many events. The analysis of this data, which has just begun, will yield a result with two times smaller uncertainty and this much smaller error will eliminate the possibility of a statistical fluke if the central value of the measurement remains within the present quoted error limits.
(2) The Standard Model theory prediction is right, but new data from other particle physics experiments used by the model will change it. Although the uncertainty in the current calculation is smaller than the experimental measurement, one part of the Standard Model theory is particularly difficult to determine and involves the analysis of related data from many experiments at positron-electron colliders. New data obtained recently at accelerators in Russia, China, and the U.S., which has not so far been included in the Standard Model theory, will soon reduce the Standard Model uncertainty considerably.
(3) Finally, one could conclude that the Standard Model is either incomplete or wrong. In that case, it would be necessary to revise the theory. What the E821 measurement does is make a statement that "there is new physics out there and it affects the muon g-factor at a certain level." The measurement does not say what that new physics is likely to be. Of course, many theorists have already considered this possibility and have suggested that supersymmetry, muon substructure, or W-boson substructure would very likely affect the muon g-factor. In any case, the information bodes very well for the startup of the next run of the Tevatron Collider at the Fermi National Accelerator Laboratory and, later in the decade, for the new Large Hadron Collider (LHC) at CERN, as well as for a very high energy electron-positron collider or a muon collider. These colliders will be able to make "direct" discoveries of new particles of high mass that are not now part of the Standard Model of particle physics.
Some Vocabulary and Terms
Muon: Essentially, a "heavy" electron. The muon g-2 test is 40,000 times more sensitive to the Standard Model extensions compared to the electron. However, the electron g-factor has been measured to about 4 parts per billion (ppb) already. The muon, electron, and tau are generically referred to as charged leptons, and they have the remarkable property that they are believed to be point particles. That is, they donit have any root physical structure and they are not made out of any smaller building blocks, although the presence of electric and other fields do give them some dimension. Contrast this with, say, a proton, which is made up of quarks. The electron is a stable particle, while the muon and tau are radioactive and decay after some period of time. Electrons are all around us, and some muons (and even taus) are produced by cosmic rays. To obtain the number of muons necessary to measure the muon g-2, however, they must be produced by collisions of high-energy particles in a laboratory.
Spin: All muons spin on their axes like a toy top or the earth on its polar axis. All muons spin at the same rate. When we speak of spin direction we mean the direction of the axis of rotation. Polarization: In a collection of a large number of muons, if the spin directions are random, we would say that they are "unpolarized." On the other hand, if their spins tend to be in one particular direction on average, we say that they are "polarized." In the muon g-2 experiment, when the muons are first injected into the storage ring, they are polarized along their direction of motion.
Magnetic moment: The muon has a magnetic moment, which is equivalent to saying it has a north and south pole just like a bar magnet or a compass. The north and south poles of the muon magnet are aligned along the direction of the spin. The strength of the magnet is indicated by the magnitude of the magnetic moment. Its value is sensitive to detailed properties of the muon, and its measurement is an excellent test of models which predict these properties.
Spin precession: The familiar toy top kit consists of a gyroscope and a stand to support it. Suppose that the top's axis is in the horizontal plane. The support point of the top is on the axis of rotation, but away from the center of mass, so that gravity will exert a torque which tends to align the axis with the direction of gravity (the top will fall down). If the top is not spinning, this is exactly what happens — the top falls down. On the other hand, if the top is spinning, the axis of the top precesses slowly in the horizontal plane instead of aligning with the gravitational force. The rate of precession will depend on the force of gravity (its torque) and on how fast the top is spinning.
In the g-2 experiment, the magnetic field in the storage ring is vertically oriented. When the muons are injected into the storage ring, their spin axes are in the horizontal plane (in fact they are aligned with their direction of motion). The north-south poles of the muon magnet are aligned with the spin direction, so the magnetic field will exert a torque which tends to align the spin axis with the direction of the field, just like a compass or bar magnet would align along the field. If the muon were not spinning, this would be exactly what happens. On the other hand, the muon is spinning, so the axis of the muon precesses slowly in the horizontal plane instead of aligning with the magnetic field. The rate of precession will depend on the force of the magnetic field (its torque), the size of its magnetic moment, and on how fast the muon is spinning.
g-factor: The magnetic moment is proportional to the dimensionless quantity g and fundamental constants, including the inverse of its mass.
g-2: The most rudimentary theory would predict that the value of g for the muon would be 2 (Dirac theory). More complete treatments, using more advanced theories, predict that g-2 is on the order of one part in 800, and experiments have confirmed this to high precision. The quantity a_mu =(g-2)/2 is called the "anomaly." If g were exactly 2, then the muon spin, if initially directed along the muon's momentum, will turn at the same rate as the muon around the ring, and will remain aligned with the muon momentum. In the muon g-2 experiment we measure the rate at which the muon spin changes direction compared to the rate at which the muon momentum changes direction — in other words, we measure g-2, not g. If we measure g-2 to 1.3 parts per million of itself, then we measure g, and therefore the size of the magnetic moment, to about 2.6 parts per billion!
Standard Model: The Standard Model is a model of the basic building blocks of matter (quarks, leptons) together with the particles that mediate the electromagnetic force (gauge bosons, e.g. W, Z, photons, gluons), the strong force (the powerful force which holds nuclei together), and the weak force (much weaker than either the strong or electromagnetic force, and responsible, for example, for the decay of the muon). Gravity is the fourth force, but has not yet been incorporated into the Standard Model, and is so much weaker than the other forces that it is not believed to be of any consequence in the muon g-2. The Standard Model predicts virtually all known experimental results. But in many ways, the Standard Model is considered unsatisfying, since we donit really know why we have the basic particles, and the model is not able to predict such things as their masses (the masses are believed to come from the so-called Higgs mechanism, the subject of study of many high-energy experiments, yet to be demonstrated).
Beyond the Standard Model: There are a number of potential theories which modify the Standard Model. For example, there is supersymmetry, which predicts a partner for every known particle. Every fermion would have a boson partner, and every boson would have a fermion partner. So far, none of these hypothesized partners have been seen. Under certain scenarios, the existence of such particles would have a slight effect on g-2. If the measured value of g-2 differs from the Standard Model prediction, then supersymmetry is one of the possible explanations. Another possibility is that the muon is not a point particle after all, but is in fact constructed of as yet unknown smaller particles. Or, the W gauge boson may have a g value which differs from 2. These are usually listed as the most likely explanations for any discrepancy between the Standard Model and the measured value of g-2, but perhaps none of them is right!
2001-20879 | INT/EXT | Newsroom