Computation and Data-Driven Discovery (C3D) Projects
Replicating Machine Learning Experiments in Materials Sciences
To harness the benefits of new-generation machine learning (ML) algorithms in materials informatics and broaden the path of accelerated discovery, it is necessary to understand their limits and establish transparency in how results are obtained. Better ways of explaining results obtained with ML methods will lead to improved reproducibility of results in materials science and more confidence in the ability of ML methods to predict new candidates for experimentation. Transparency and reproducibility are important aspects of validation for ML models that are not fully understood and applies across the board independent of the application domain. Understanding the limits of computational reproducibility when dealing with complex mathematical models, such as ML models, extends beyond making accessible scientific code, training data, and hyperparameters. ML methods present specific challenges in reproducibility related to the building of models, the effects of random seeds, and the choice of platforms and execution environments.
This reproducibility experiment is investigating the reproducibility of previously published results by one of the study’s co-authors (Supervised Machine-Learning-Based Determination of Three-Dimensional Structure of Metallic Nanoparticles, 2017. DOI: 10.1021/acs.jpclett.7b02364). We are studying reproducibility across ML platforms and the influence of random factors in two types of widely used regression models: 1) gradient boosted trees (GBT), an efficient ML model that ensembles a set of decision trees and 2) multilayer perceptron (MLP), a classic fully connected neural network. These models showed the highest performance in the original results.
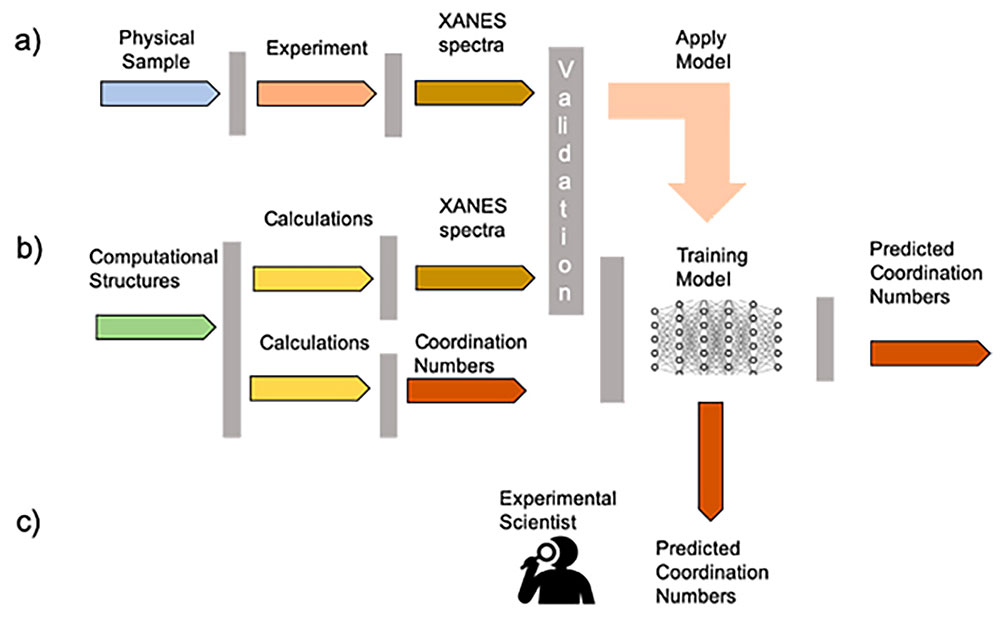
Figure 1: Schematic for applying machine learning to guide high-throughput experiments.
In materials science, ML methods are increasingly used to predict the relationship between atomic structures and materials properties, as well as to provide guidance to experimentalists for suggesting potentially useful combinations. In the previously published results, ML models were used to predict Coordination Numbers (CN) known to characterize size and three-dimensional (3D) shape of nanoparticles. Training sets are built using computational data produced from ab initio methods. The model then can be used on experimental spectra to help determine the properties of experimental particles. In the experimental process, X-ray absorption near edge structure (XANES) spectra, a type of property, are measured and CN are calculated. The computational approach calculates XANES spectra and CN from computational structures. After validation, computational XANES spectra and CNs are used to train the model. Predicted CN are compared to calculated CN to validate the model. In the ML approach, the trained model can be used with large amounts of experimental spectra pouring out of high-throughput detectors to predict expected CN during the course of an experiment (Figure 1).
For the CN prediction task, we measure the influence of one random factor at a time by fixing all of the hyperparameters and other random factors (with the appropriate random seeds) and free the factor under consideration. For MLP, we investigate the different data order when using stochastic gradient descent to iteratively optimize the loss function and different weight initializations. For GBT, the influence of random feature and data selections are studied. The models are trained five times for each case to obtain an accuracy number on the test data. Table 1 provides some results.
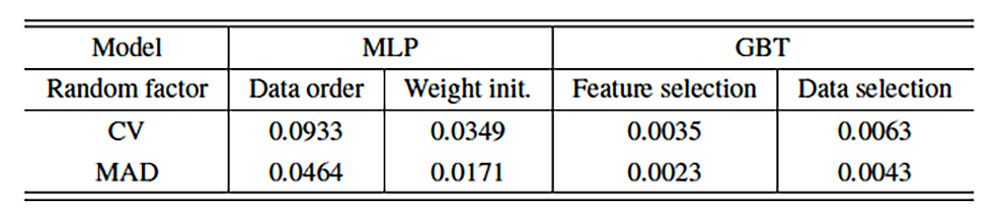
Table 1. Results of replicating the Coordination Number prediction task with various random factors.
Coefficient of Variation (CV), also known as Relative Standard Deviation, and MAD (Mean Absolute Difference (MAD) are the metrics used to disperse accuracy numbers. As these metrics show, GBT appears more robust than MLP, i.e., with a certain amount of randomness, the accuracy of GBT is more consistent than MLP. Yet, in the artificial intelligence (AI) literature, results showing the best performance usually are the ones reported, regardless of the robustness of the performance.
It is common knowledge that training an ML model multiple times, even with the same dataset, does not usually produce the same model as different training and testing errors are produced with each run. A second set of errors referring to transfer learning or domain adaptation typically draws more attention from ML researchers. Our experiment shows that the first class of errors should not be ignored by practitioners and scientists interested in the practical application of these models for their domain science.
Publications
Pouchard, L., Y. Lin, and H. van Dam, “Replicating Machine Learning Experiments in Materials Sciences,” ParCo Symposium 2019, DOI: 10.3233/APC200105.




