RHIC Accelerators
The Relativistic Heavy Ion Collider complex was composed of a long “chain” of particle accelerators
Heavy ions began their travels in the Electron Beam Ion Source accelerator. The ions then traveled to the small, circular Booster where, with each pass, they were accelerated to higher energy. From the Booster, ions traveled to the Alternating Gradient Synchrotron (AGS), which then injected the beams via a beamline into the two rings of RHIC. In RHIC, the beams got a final accelerator “kick up” in energy from radio waves. Once accelerated, the ions could orbit inside the rings for hours. RHIC could also conduct colliding-beam experiments with polarized protons — these were first accelerated in the Linac and were then ramped up to higher energies in the Booster, AGS, and RHIC. All the pre-injection accelerators and one of RHIC’s ion storage rings will be reused for the Electron-Ion Collider (EIC), a new facility under construction at Brookhaven Lab.
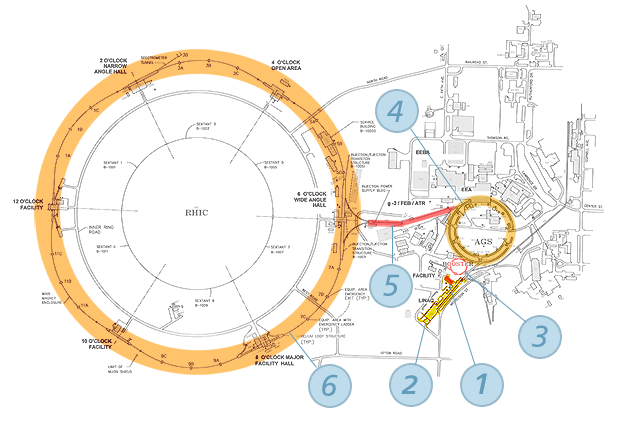
1. Electron Beam Ion Source (EBIS)
EBIS is a compact source and heavy ion accelerator that served as the start of the pre-injector system for RHIC and continues to be operational for the NASA Space Radiation Laboratory (NSRL). It will also be used for the EIC. EBIS can create highly charged ion beams from almost any element. These ion beams are then accelerated by two small linear accelerators and carried to the Booster. EBIS can feed beams of different ions to the collider’s large ion storage ring(s) and NSRL at practically the same time, and also quickly switch between different ion species.
2. Linear Accelerator (Linac)
In addition to heavy ions, some experiments at RHIC and the future EIC used/will use colliding beams of protons. For these experiments, energetic protons are supplied by the 200-million electron volt (MeV) Linac. Protons from the Linac are transferred to the Booster.
3. Booster Synchrotron
The Booster synchrotron is a powerful circular accelerator that provides the ions more energy, by having them “surf ride” on the downhill slope of radio frequency electromagnetic waves. The ions are propelled forward at higher and higher speeds, getting closer and closer to the speed of light. The Booster then feeds the beam into the Alternating Gradient Synchrotron.
4. Alternating Gradient Synchrotron
As ions enter the Alternating Gradient Synchrotron (AGS) from the Booster, they are traveling at about 37% the speed of light. As they whirl around the AGS and are accelerated as in the Booster, the ions gain even more energy — until they are traveling at approximately 99.7% the speed of light. Light travels at about 186,000 miles per second, the natural speed limit in the universe. This is the reason for the “relativistic” part of RHIC's name and will continue to be an important feature of the EIC.
5. AGS-to-RHIC Line
For RHIC operations, when the ion beam reached top speed in the AGS, it was taken down another beamline called the AGS-to-RHIC (AtR) transfer line. At the end of this line, there was a “fork in the road,” where a switching magnet sent the ion bunches down each of two beamlines to fill RHIC's two ion storage rings. Bunches directed left filled the clockwise RHIC ring while those directed right traveled counterclockwise in the second RHIC ring. From there, the counter-rotating beams were accelerated further to reach 99.995% the speed of light. Since the EIC will use only one ion storage ring, this transfer line is being reconfigured to feed beams to only that ring.
6. RHIC
RHIC’s 2.4-mile ring had six intersection points where its two rings of accelerating magnets crossed, allowing the particle beams to collide. Detectors were originally located at four of these “interaction regions,” and later, at only two. The detectors picked up fleeting signals produced by particles streaming from the collisions, providing physicists with information about the most fundamental workings of nature. Learn about the changes that will transform this part of the accelerator complex into the EIC.
