eRHIC: An Ultra-High-Resolution Electron Femtoscope
June 27, 2011
By Salvatore Fazio, Tobias Toll, and Thomas Burton

(From left) Salvatore Fazio, Thomas Burton and Tobias Toll are post-docs working in the EIC Task Force.
eRHIC is a proposed upgrade to RHIC involving the addition of a high-intensity electron beam, which will collide with one of the existing hadron beams. Such an upgrade will open a wide new frontier of precision hadron physics for the RHIC facility.
To date, the only lepton-proton collider was the HERA accelerator that operated at the DESY laboratory in Hamburg, Germany, until July 2007. Among its important contributions were measurements of the momentum distributions of partons (quarks and gluons) in the proton, via the process of deep inelastic scattering (DIS) (see figure). eRHIC is intended as the next generation lepton-proton and lepton-nucleus collider. The machine will provide polarized electrons with energies of 5-30 GeV, polarized protons with energies of 50-325 GeV, and heavy ions at up to 130 GeV/u. These beams will collide at a luminosity of the order of 1034 interactions cm2 s-1, more than two orders of magnitude higher than at HERA. The new dedicated eRHIC detector (see figure) will be nearly hermetic and will deliver high energy, momentum and angular resolutions. This opens the opportunity for very high precision measurements, allowing detailed investigations of the proton and nuclear hadronic substructures, as well as the spin structure of nucleons.
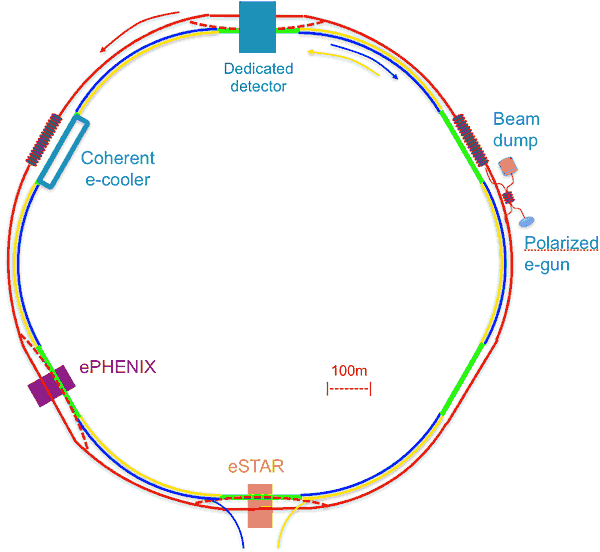
The proposed layout of eRHIC. The electron ring (red) would be added to the existing hadron rings (blue and yellow). Collisions could take place at PHENIX, STAR and at another interaction point with a new dedicated eRHIC detector. Polarized electrons would be accelerated by multiple passes through a pair of LINACs, collide with the hadron beam, and then be dumped.
Deep inelastic scattering (DIS) is a type of collision between an electron and a proton. In DIS, the electron scatters, interacting with a single quark in the proton via exchange of a virtual photon. Q2 is the invariant mass of the photon, and represents the resolution at which the proton is probed. x is the fraction of the proton’s longitudinal momentum carried by the struck quark.
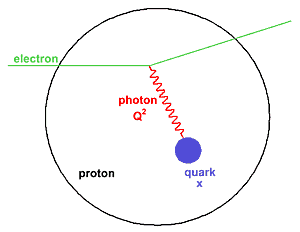
The quark (and usually the proton remnant) subsequently break up into hadrons. The beauty of DIS is that Q2 and x can be determined simply by measuring the scattered electron. Additional information about the collision can be found by also measuring one or more of the produced hadrons. If only the electron is detected, the measurement is said to be inclusive. If one or more hadrons are also detected, it is said to be semi-inclusive. If every final-state particle is detected, the measurement is said to be exclusive.
In this article we summarize the physics case for the EIC in a comprehensive way, and highlight a few of the most important measurements in the very rich physics program of eRHIC.
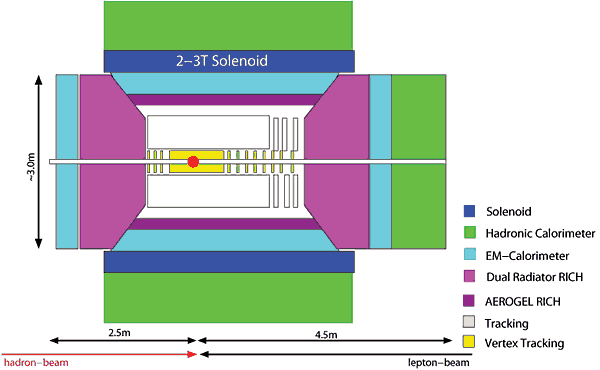
A proposed dedicated detector at eRHIC consists of: a solenoidal field in the barrel region at mid-rapidity; silicon tracking with full rapidity coverage around the interaction point; Cherenkov detectors for particle identification; and both electromagnetic and hadronic calorimeters. A dedicated spectrometer can be installed along the beam-pipe in the direction of the outgoing proton to measure those protons scattered at very small angles.
Probing the gluon content of ions and protons at small x
Protons and neutrons are bound by the strong nuclear force, which is mediated by gluons and described by the theory of quantum chromodynamics (QCD). Unlike photons, which mediate the electromagnetic force, gluons can interact with each other. It is this self-interaction that generates around 99% of the visible mass in the universe, while only the remaining 1% is provided by the intrinsic masses of quarks. The existence of the gluon was experimentally confirmed in 1979 at the PETRA accelerator at DESY, in three-jet events in high energy electron-positron collisions. Even though gluons were discovered three decades ago, the force they mediate remains the least well-known in the standard model of particle physics.
One of the outstanding puzzles in our understanding of the theory of the strong interaction is its behavior at small values of x. At HERA it was found that at small x the proton's content is dominated by gluons. Small x means a gluon carries a small fraction of the proton's momentum, which means that the momentum is shared among many gluons. However, there is a puzzle: extrapolations of the present measurements to ever-smaller x yield an ever-rising gluonic cross-section. Thus, the gluonic part of the cross section will eventually become larger than the total cross section. Such unlimited growth is mathematically impossible; there has to be a mechanism that tames this rise. This mechanism is called saturation. Put simply, small x means the proton contains many gluons, all with a small momentum fraction. In quantum mechanics small momentum means large wavelength. This means that the wave functions of the gluons start to overlap, and two overlapping gluons can recombine into one, hence reducing the number of gluons. There are many models and calculations describing these phenomena, but there is as of yet no conclusive measurement of saturation. Such a measurement requires probing the proton at sufficiently small x and Q2 that saturation phenomena manifest. This has been the problem in past accelerator experiments, since they were unable to access the required small x and Q2. There are two ways to make these saturation phenomena accessible via experiments: to increase the energy in the collisions, by building new electron-hadron accelerators; or to use heavy ions instead of protons. When an electron collides with an ion at high energy, it does not see a ball of A nucleons. Rather, the ion appears Lorentz contracted into a “pancake”. At small x, the wavelength of the probe exceeds the size of the nucleus, such that the probe cannot distinguish between the individual nucleons. It therefore interacts with many nucleons at once, which has the effect of increasing the saturation scale, i.e. the value of Q2 below which saturation occurs, by a factor proportional to A1/3. This is how eRHIC would be able to measure saturation.
Saturation most probably already plays an important role in RHIC and LHC experiments, but probing hadronic matter with hadronic matter does not provide enough control of the kinematics of a collision to give conclusive answers about these phenomena. Like Richard Feynman once said: “Scattering protons on protons is like colliding Swiss watches to find out how they are built”. Using an electron as a probe gives this required control.
Measuring the Momentum Structure of the Nucleus
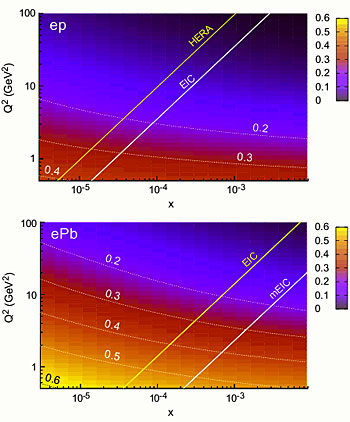
A measure of gluon density within protons (top) and a lead nucleus (bottom). Purple means dilute and orange means dense. A density of 0.5 corresponds to the saturation scale. Under the lines are the Q2 and x values accessible at HERA and at eRHIC. eRHIC can probe below the saturation scale in e-A collisions.
One of the key measurements in electron-ion (e-A) collisions at eRHIC is also one of the simplest: the measurement of the scattered electron alone while ignoring all other particles produced in the interaction. What is then measured are called the structure functions of the nucleus or proton. In these inclusive measurements the cross-section is probed as a function of x and the probing scale Q2. These are momentum variables and hence probe the momentum distribution of the content of the nucleus. For small x these structure functions depend directly on the gluon content of the nucleus, and thus will reveal saturation phenomena when comparing results from e-p and e-A collisions. The figures below show the increase of the cross-section in regions of x and Q2. The color in the graphs indicate the density of gluons in the proton and nucleus. At the saturation scale this density measure is close to 0.5. It can be seen in the figures that in e-p the saturation scale is not reached, even at HERA, but when the electron collides with a heavy nucleus, e.g. lead, eRHIC will be able to reach a probing scale below the saturation scale, which happens at small x and Q2. It is in this dense region where saturation will be found.
These measured structure functions can be used to extract parton density functions (PDFs), which describe how gluons and different kinds of quarks are distributed within the proton/nucleus as a function of x and Q2. These PDFs play a very important role as an input in many theoretical calculations in high energy particle physics.
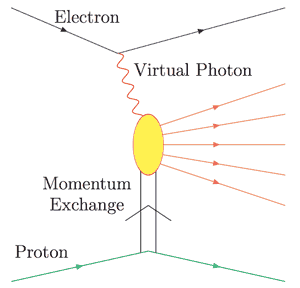
In a diffractive event the proton or ion stays intact in the collision. There may however be an exchange of momentum between the proton and electron.
An almost as simple measurement is that of diffractive structure functions. In diffraction the proton or ion stays intact after the collision with the electron, but the collision still produces one or many extra final state particles. For this to happen the virtual photon interacts with the ion via an exchange of momentum but not of quantum numbers (see figure). In e-A collisions at eRHIC around 30% of the interactions are expected to be diffractive. The diffractive structure functions are determined by only measuring the scattered electron and the scattered proton/nucleus. At small x, the diffractive structure functions depend on the square of the gluon content, making them an even stronger observable for a measurement of saturation than normal structure functions.
These inclusive measurements are considered to be golden measurements in the small-x physics program of eRHIC. If we probe saturation with these measurements it will show up as a plateaux in the cross-section when probed at ever smaller x.
Spatial mapping of the nucleus
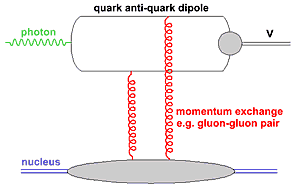
In exclusive production of vector mesons, the virtual photon splits into a quark anti-quark dipole, which interacts with the nucleus diffractively.
The spatial distribution of protons within the nucleus has long been known. But how are the gluons in the nucleus distributed in space? At eRHIC this can be determined by detecting the exclusive production of a so-called vector meson in diffractive events. In these events the virtual photon splits into a quark anti-quark dipole, which interacts with the nucleus diffractively (see figure). In these collisions the nucleus stays unchanged, though it may subsequently break up. If the exchanged momentum corresponds to a resonance in the nucleus, the probability that the nucleus remains intact becomes small. By measuring where these resonances appear as a function of the exchanged momentum, one can extract the transverse spatial distribution of gluons within the nucleus. This has never been measured before, but can be done at eRHIC with very high precision.
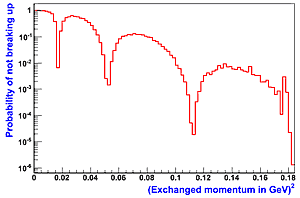
The probability of a gold nucleus not breaking up when only a J/Ψ meson is produced in a diffractive event. The dips where the probability becomes small correspond to resonances in the nucleus. The positions of these are then used to extract the spatial distribution of gluons.
3-dimensional imaging of the proton
Structure functions and parton distribution functions of the nucleons, investigated at the HERA accelerator, represent only special cases of a more general, much more powerful, way to characterize the structure of the nucleon: generalized parton distributions (GPDs) and the transverse-momentum-dependent parton distributions (TMDs). In fact, PDFs discussed above are limited to the longitudinal momentum distributions, neglecting any transverse component, whereas in the GPD and TMD approaches one obtains a 3-dimensional picture of the nucleon, respectively in impact-parameter and transverse momentum space (see figures below).
eRHIC will be equipped with a full-acceptance detector which will be able to measure inclusive, semi-inclusive and exclusive reactions. TMDs can be extracted from semi-inclusive DIS data for different spin-dependent and spin-independent observables, as will be discussed below. eRHIC would allow extremely precise studies of TMDs. Furthermore, they may clarify our currently rudimentary understanding of the associated, surprisingly large, azimuthal asymmetries in particle production found at DESY, CERN, BNL and JLab, through detailed studies of their Q2 dependence.
GPDs are functions describing the distribution of quarks and gluons in the nucleon with respect to both position and momentum. The concept of GPDs has revolutionized the way scientists think about the structure of the nucleon, leading to completely new methods of “spatial imaging” of the nucleon in the form of genuine 3-dimensional images. Moreover, GPDs allow us to study how the orbital motion of quarks in the nucleon contributes to the nucleon spin - a question of crucial importance for nucleon structure.
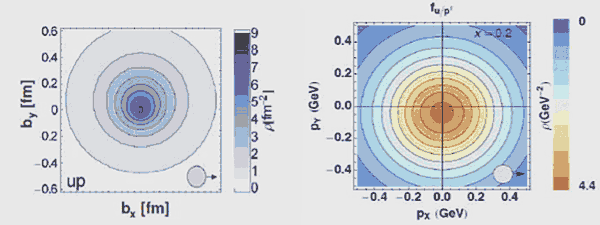
The GPDs (left) and TMDs (right) provide a 2+1-dimensional image of the gluons in the nucleon.
Measurements of GPDs in hard exclusive processes with an e-p/e-A collider require substantially higher luminosities than traditional inclusive DIS because of the small cross sections and the need for differential measurements. The detectors and the interaction region must also be designed to permit full reconstruction of the final state. The dependence of the cross section of exclusive production of certain particles on the four-momentum transfer to the proton/nucleus contains information about the transverse spatial distribution of gluons and quarks. The complete structure of the proton is described by a large number of GPD functions, for both quarks and gluons. These can be accessed by measuring the production of different types of particles (e.g. J/Ψ). So called DVCS, in which the produced particle is a photon, is a particular “golden” measurement because it shows a clean experimental signature and it is not affected by the large uncertainties coming from the lack of knowledge of the vector meson’s wave-functions. Analyzing DVCS together with J/Ψ, which probes the gluon distribution alone, one can disentangle the quark and gluon GPDs, and test the evolution of the GPDs predicted by QCD. The differential cross-section for DVCS, as well as for the other exclusive channels, has been measured at HERA. However, the HERA detectors were not optimized for this physics and were unable to measure the final-state particle with sufficient resolution. Comprehensive parton imaging in the nucleon requires precise measurements of the impact parameter for a wide range in x, currently beyond the capability of any collider. Building eRHIC with a properly designed detector would finally make this possible. Moving from HERA to eRHIC will have the same impact as moving from an old black and white picture to a 3-D high resolution image.
Probing the proton’s spin structure
Spin, the intrinsic angular momentum arising from quantum mechanics, is a fundamental property of particles. While the proton has long been known to have a spin of half a unit of ħ, understanding how this total arises from the partons that comprise the proton remains elusive. Consider a proton with a particular helicity, that is with its spin either aligned with or opposite to its momentum. Its total helicity (1/2ħ) must be composed of contributions from both the intrinsic spins and orbital angular momenta of the quarks and gluons within. Contrary to early expectations, the spin of the quarks alone does not account for the majority of the proton spin; in fact, only some 30% can be ascribed to quark spin. The remainder must therefore be due to the spin of gluons and the orbital angular momentum of quarks and gluons. How the spin is distributed among these sources is a major question in QCD; one that eRHIC intends to address.
The contribution of the gluon spin has already been a topic of intense study in both DIS experiments and here at RHIC, in the p-p programs of PHENIX and STAR. The gluon spin contribution can be determined from measurements of the gluon helicity polarization (i.e. the difference in the number of gluons polarized along vs. opposite the proton helicity), referred to as Δg. Existing measurements yield a gluon contribution that is close to zero, though the uncertainties remain large. Does this then mean that the gluon spin contributes little to the proton spin? Not necessarily. Existing measurements cover only a small range in x (see figure), therefore we only know that the gluons in this range give a small contribution. The gluon distribution at smaller values of x, where no experimental data currently exist, is essentially unconstrained. Thus the gluons in this region could carry a significant quantity of spin. A major aim of eRHIC will be to measure the gluon helicity distribution in this region, down to values of x of 10-4 or lower, with heretofore unattainable precision. At this point, the total gluon contribution to the proton spin can be well constrained, at the level of 10% or better. Only then will we know if the gluon spin is a major or minor contributor to the spin of the proton.
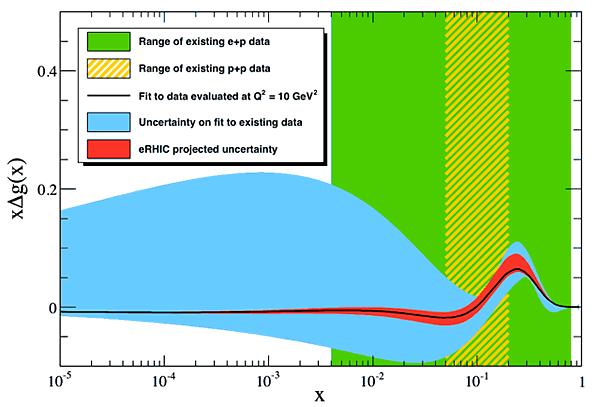
The distribution xΔg, when integrated over all x, gives the contribution of gluon spin to the proton spin. Existing data cover only a small x range (green, yellow). The fit to these data (black line) has very large uncertainties at small x (blue), so the total spin contribution is largely unknown. Precise eRHIC measurements will greatly reduce these uncertainties (red) so the gluon contribution will be known.
Like the gluon, the helicity distributions of sea quarks are also poorly constrained by existing data. The portions of strange and anti-strange quarks are particularly poorly understood; the anti-quark contribution cannot in fact be distinguished from the quark contribution with current data. eRHIC will use semi-inclusive DIS to perform a full and precise flavor (e.g. up, down or strange) decomposition of the sea quark spin. This is done by using a hadron produced in the collision as a ‘tag’ on the flavor of the quark involved in the initial interaction. As an example, a π+ observed in the final state has a valence quark structure of (u, anti-d), and is therefore more likely to have originated from a u or an anti-d quark rather than their respective charge conjugates. Truly disentangling the flavor structure will require measuring a variety of different hadron species (π+, π-, K+, K-...) over a broad span of kinematics, but the precision achievable at eRHIC will allow the individual contributions from u, anti-u, d, anti-d, s and anti-s quarks to be precisely separated and quantified.
In all the above we have talked about helicity: a proton with its spin aligned with or against its momentum vector, and partons with spin aligned with or against this same longitudinal direction (i.e. longitudinally polarized). However, if we consider a proton with spin aligned perpendicular to its momentum vector (i.e. transversely polarized), we open up an entirely new range of rich QCD phenomena, some even less well understood than in the longitudinally polarized case. It is known from numerous experiments, from over twenty years ago up to the present RHIC era, that the hadrons produced in collisions involving a transversely polarized proton exhibit a non-uniform azimuthal angular distribution. Initial expectations from QCD calculations expected such phenomena to be heavily suppressed, whereas experiments demonstrate huge asymmetries up to 40%. Much experimental and theoretical effort has gone into understanding this. A description potentially exists based on a family of transverse-momentum-dependent distribution functions (TMDs).
Conventional parton distribution functions (PDFs) describe parton distributions in terms of x and Q2 only. Similarly, fragmentation functions (FFs) describe the fragmentation of partons into final-state particles in terms of only the momentum of the produced particle. TMD-PDFs and TMD-FFs add a transverse momentum dimension, and correlate the spin of the proton with both the spin and transverse momentum of the partons within it (in the case of TMD-PDFs) or of the hadrons produced (TMD-FFs). Measurements by experiments such as HERMES, COMPASS and BELLE have demonstrated that a number of such distribution functions exist, but present data is rather limited in its precision. eRHIC will be ideally suited for exploring the entire family of such TMDs, because of its extremely high luminosity and the access it provides to a wide range of kinematics. In particular, the quark and gluon sea, presently unconstrained by data, can be probed in detail. TMDs are of interest not just for their relation to the proton spin, but because they allow a 3-dimensional imaging of the proton, in both longitudinal and transverse momentum space. TMD-PDFs also have an important relation to orbital angular momentum, as their existence requires the orbital motion of partons. Furthermore TMDs possess a rich set of features that fundamentally test our understanding of the QCD formalism.
2011-2465 | INT/EXT | Newsroom








