sPHENIX Gets CD0 for Upgrade to Experiment Tracking the Building Blocks of Matter
First step on a path toward a detector with unprecedented capabilities for deciphering how the properties of the hottest matter in the universe emerge from the interactions of its fundamental particles
January 13, 2017
The U.S. Department of Energy (DOE) has granted “Critical Decision-Zero” (CD-0) status to the sPHENIX project, a transformation of one of the particle detectors at the Relativistic Heavy Ion Collider (RHIC)—a DOE Office of Science User Facility at Brookhaven National Laboratory—into a research tool with unprecedented precision for tracking subatomic interactions. This decision is an important first step in the DOE process for starting new projects, stating that there is a “mission need” for the capabilities described by the proposal.
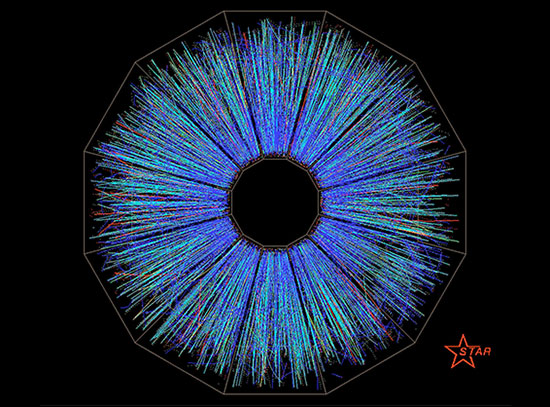
“We are very excited that the Department of Energy has recognized the importance of the sPHENIX project,” said Berndt Mueller, Associate Laboratory Director for Nuclear and Particle Physics at Brookhaven. “This upgrade will offer new insight into how the interactions of the smallest building blocks of matter give rise to the remarkable properties of ‘quark-gluon plasma’—a four-trillion-degree soup of fundamental particles that existed in the universe a microsecond after its birth and recreated regularly in particle collisions at RHIC.”
As Brookhaven Lab physicist Dave Morrison, a co-spokesperson for the sPHENIX collaboration, explained, “sPHENIX will be an essential tool for exploring the quark-gluon plasma, including its ability to flow like a nearly ‘perfect’ liquid. The capabilities we develop and scientific insight we gain will also help us to prepare for the coming research directions in nuclear physics,” he said.
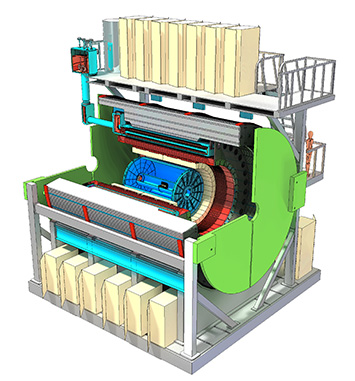
The sPHENIX project is an upgrade of RHIC’s former PHENIX detector, which completed its data-taking mission in June 2016.
“We’ll be leveraging scientific and financial investments already made when building RHIC,” said Gunther Roland, a physicist at the Massachusetts Institute of Technology and the other co-spokesperson for sPHENIX. “But at the same time, the transformation will introduce new, state-of-the-art detector systems.”
With a superconducting solenoid magnet recycled from a physics experiment at DOE’s SLAC National Laboratory at its core, state-of-the-art particle-tracking detectors, and an array of novel high-acceptance calorimeters, sPHENIX will have the speed and precision needed to track and study the details of particle jets, heavy quarks, and rare, high-momentum particles produced in RHIC’s most energetic collisions. These capabilities will allow nuclear physicists to probe properties of the quark-gluon plasma at varying length scales to make connections between the interactions among individual quarks and gluons and the collective behavior of the liquid-like primordial plasma.
Conceptual studies and R&D are already underway for key components, including the solenoid, calorimeters, and tracking detectors. The CD0 decision—the go-ahead that enables conceptual design and R&D to proceed—will enable these efforts and set sPHENIX on the path toward an exciting physics program starting in 2022.
Research at RHIC and the sPHENIX project are supported primarily by the DOE Office of Science.
Brookhaven National Laboratory is supported by the Office of Science of the U.S. Department of Energy. The Office of Science is the single largest supporter of basic research in the physical sciences in the United States, and is working to address some of the most pressing challenges of our time. For more information, please visit science.energy.gov.
2017-6793 | INT/EXT | Newsroom