A New Quantum Algorithm for Quantum Chemistry
CFN and Stony Brook University researchers propose a new quantum algorithm to accurately solve the total energies of molecules
September 30, 2022
 enlarge
enlarge
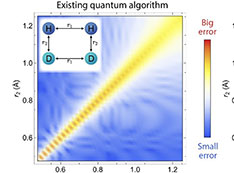
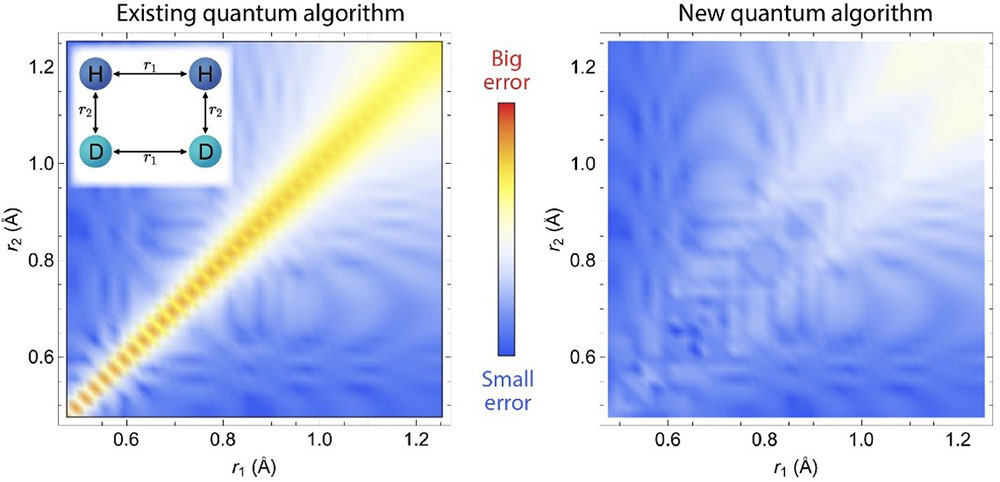
Comparison between the new (GeoQAE) and existing algorithm, showing the energy difference compared to the exact results is very small in GeoQAE for a chemical reaction with two pairs of molecules (left inset). The axes represent the distances between atoms.
Scientific Achievement
Through the BNL-led Co-design Center for Quantum Advantage (C2QA), a team of scientists at Stony Brook and CFN proposed a new quantum algorithm to accurately solve total energies of molecules.
Significance and Impact
This work will find application in quantum chemistry, such as predicting reaction energies and lowering barriers for future quantum devices by tackling the limitations caused by energy level crossings and energy gap closing.
Research Details
Quantum algorithms have been successfully applied in quantum chemistry to obtain the ground-state energy of small molecules. Although accurate near the equilibrium geometry, the results can become unreliable when the chemical bonds are broken at large distances. For any adiabatic approach, this is usually caused by serious issues, such as energy gap closing or level crossing along the adiabatic evolution path. This work proposes a quantum algorithm based on adiabatic evolution to obtain molecular eigenstates and eigenenergies in quantum chemistry, which exploits a smooth geometric deformation by continuously varying bond lengths and bond angles. The team demonstrates its utility in several examples on a noiseless quantum simulator, including H2O, CH2, and a chemical reaction of H2+D2→ 2HD, by uniformly stretching chemical bonds. The new algorithm solves the problems related to energy gap closing and level crossing along the adiabatic evolution path at large atomic distances. The new method performs more stably and achieves better accuracy than previous adiabatic methods and the fidelity analysis demonstrates that even with finite bond length changes, the new algorithm still achieves high fidelity for the ground state.
- Ground-state and low-lying excited state energies were obtained with several orders of magnitude higher accuracy, yields an energy curve in agreement with the exact solution.
- New algorithm (Geometric Quantum Adiabatic Evolution) was used to simulate the potential energy surface for H2O, CH2, and a chemical reaction with two pairs of molecules (H2 + D2 → 2HD)
- The CFN Theory and Computation facility was for the quantum chemistry applications.
Publication Reference
Hongye Yu, Deyu Lu*, Qin Wu, Tzu-Chieh Wei*, “Geometric quantum adiabatic methods for quantum chemistry.” Physical Review Research 4, 3 (2022).
DOI: 10.1103/PhysRevResearch.4.033045
OSTI: https://www.osti.gov/pages/biblio/1876239
Brookhaven Newsroom: Quantum Chemistry Finds a New Path on Quantum Devices
Acknowledgment of Support
Part of this work (in particular the research on the connection of the maximally commuting Hamiltonian to the Hartree-Fock solution) was supported by the National Science Foundation under Grant No. PHY 1915165 (T.-C.W.). The part of the research that involves quantum chemistry applications used the theory and computation resources of the Center for Functional Nanomaterials (CFN), which is a U.S. Department of Energy Office of Science User Facility, at the Brookhaven National Laboratory under Contract No. DE-SC0012704 by the U.S. Department of Energy, Office of Science (D.L. and Q.W.). The research on the quantum algorithmic development in this work was supported by the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Co-design Center for Quantum Advantage (C2QA) under Contract No. DESC0012704 (H.Y and T.-C.W.).
2022-21055 | INT/EXT | Newsroom