Students Discover the Mathematics Within Dragonfly Wings

Because you are not running JavaScript or allowing active scripting, some features on this page my not work. >> Enable Javascript <<

High schoolers find a new example of nature's use of the "golden angle"

November 16, 2023

Researchers' calculations of polygon shapes in the venation pattern of a dragonfly wing are superimposed on a photograph of a dragonfly.

The logic of math is found in many beautiful living things: the spiral of a nautilus shell, the bloom of an artichoke, the seeds and petals of a sunflower. These patterns are nature’s way of optimizing structure, strength, and function, and they show us that the natural world, for all its apparent randomness and chaos, also contains logic and order.

At the U.S. Department of Energy’s (DOE) Brookhaven National Laboratory, a new example of math in nature has been discovered by a team of researchers who found that the “golden angle” exists in the vein pattern on dragonfly wings. Notably, the team was led by two high school students who were able to conduct research at Brookhaven via its High School Research Program (HSRP). Their work was published in a top journal, Scientific Reports—an impressive achievement.

Keene Lu and Samson Shen were students at Ward Melville High School in Setauket, New York, when they participated in HSRP internships during the summer of 2019 and spring of 2022, respectively. Lu is now studying at Northwestern University and Shen is a student at UCLA. They spearheaded the work, guided by two scientists at the National Synchrotron Light Source II (NSLS-II): physicist and beamline scientist Xiaojing Huang and senior biophysical chemist Lisa Miller. NSLS-II is a DOE Office of Science User Facility at Brookhaven Lab.

Pictured left to right are Xiaojing Huang, Keene Lu, Samson Shen, and Lisa Miller.

Nature’s golden numbers

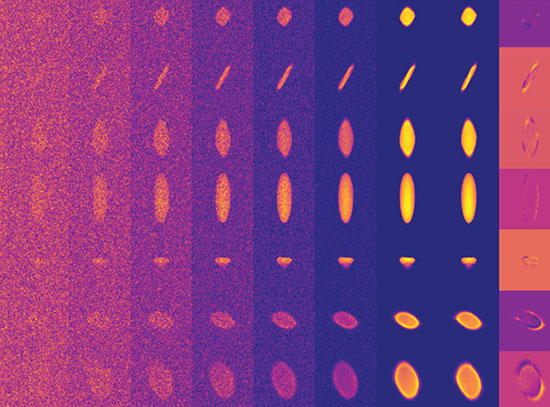
The project’s origin goes back a decade, when Huang was studying scanning probe microscopy, a method of taking a 2D image of a sample’s surface by scanning it with a physical probe. The scan creates the image point by point, typically via a grid scan, with each point in the grid separated by a fixed distance. But a scan in which the points make up concentric circles produces a better image, and Huang wondered if the scan pattern could be optimized to yield the best possible images. This led him to look for clues in nature.

There are many examples of patterns that nature has perfected and that also have a solid basis in mathematics. One of the most famous is the Nautilus shell spiral, which has proportions that are tied to the Fibonacci sequence, a series of numbers in which each number is the sum of the two before it. As the numbers get bigger, the ratio between each pair of adjacent numbers approaches the “golden ratio” of 1.618. If you factor in some circular geometry, another special number emerges: the “golden angle,” which is 137.5 degrees. The golden angle is found in many places in the natural world, especially in plants, such as in the complex spiral arrangement of petals, leaves, and seeds.

“The golden ratio and the golden angle captured my attention,” said Huang. He and his collaborators applied the spiral pattern determined by the golden angle to their scanning probe microscopy measurements and were successful in achieving the ultimate image quality. Those results were published in Optics Express in 2014.

Then, in 2018, he came across a paper that discussed the venation patterns on insect wings. The images of the dragonfly wings in the paper caught his eye, and he noticed that the vein patterns contained a lot of angles. He wondered if the golden angle could be found there. Later, he worked with Brookhaven’s Office of Educational Programs to be paired with a summer high school student intern. That is how he linked up with Lu. Huang knew that he wanted his student to investigate his hunch about the dragonfly wing images, but he left the “how” up to Lu.

enlarge

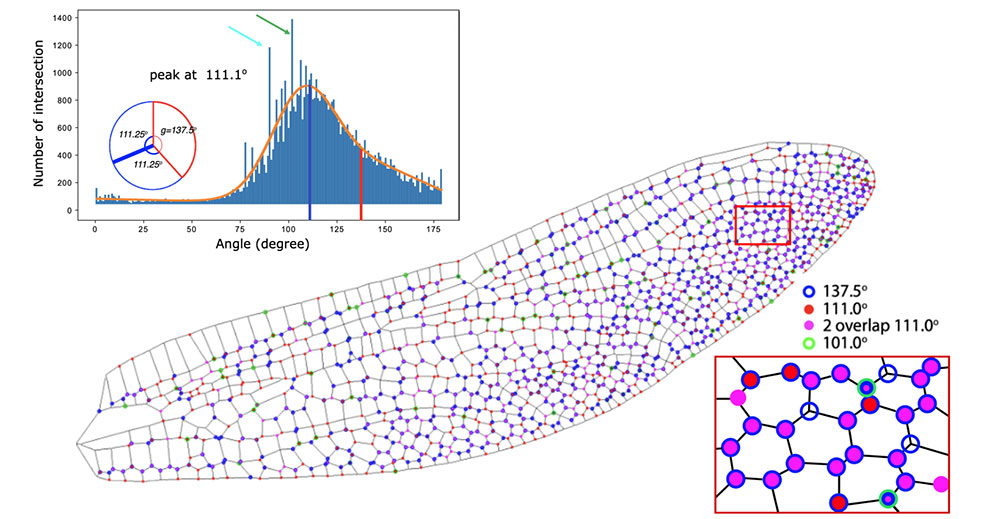
The top left image shows angular distributions of a dragonfly forewing. Researchers used a summation of two Gaussian functions to fit the skewed histograms. The peaks of the fitted curves are located at 111.1 degrees and 112.2 degrees, respectively. Considering that most vein intersections consisted of three veins, when the largest angle was the golden angle of 137.5 degrees, evenly splitting the remainder of the circle into two equal angles, as shown in the inset, the obtained angles would be 111.25 degrees, which agrees with the obtained histogram peak values. The cyan and green arrows indicate secondary peaks at 90 degrees and 101 degrees, respectively. The center image shows the locations of intersections for three specific angles on a dragonfly wing. Intersections that form 137.5 degrees (plus or minus2.5 degrees) and 111 degrees (plus or minus 2.5 degrees) are labeled in blue and red, respectively. The intersections that have two 111-degree angles (plus or minus 2.5 degrees) are labeled in magenta. Most of the blue circles overlap with magenta dots, as shown in the inset. The angle splitting at these intersections exactly follows the golden ratio as illustrated in the inset, and they are primarily observed near the trailing edge and the wing tip. Intersections forming 101 degrees (plus or minus 2.5 degrees) are labeled in green, which identify the interfacial areas connecting primary and secondary veins.

Analyzing the angles

Lu began by taking the approximately 50 dragonfly wing images from the paper and running them through image processing software to convert them to black-and-white images and narrow the vein diameters. He then sent them through a Python program, using its image processing libraries, to be “skeletonized”—reduced to bare line images.

“Keene came up with the entire imaging processing ‘recipe,’” said Huang. “I was so impressed with his self-motivation and willingness to explore different solutions.”

Next, Lu analyzed each place where the lines intersected. There were three lines per intersection and, therefore, three angles. He wrote code to find the value of those angles and, with that done for all the images, he created a plot of the distribution of those angles.

What Lu and Huang found at that point was unexpected. They did see the golden angle, confirming it could be found in the venation pattern. But the peak of the distribution—in other words, the angle that showed up most often—was 111 degrees. This angle did not immediately mean anything to them, but it was present in the vein pattern about twice as much as the golden angle.

There were also a couple of outlier angles, at 90 and 101 degrees, that disrupted the otherwise smooth distribution. Lu and Huang could not initially explain these, either.

After some analysis, they determined that the 111-degree angle was, in fact, directly related to the golden angle. If one takes a circle and subtracts out the golden angle, then divides what is left by two, the resulting angle is 111 degrees.

The 90-degree angles were even easier to explain. If one looks at the venation pattern in the images, there are several 90-degree angles at top edges of the wings. But there was no immediately clear reason for the 101-degree outliers.

Lu and Huang also noticed that the golden angle and related angles were concentrated on the bottom edges and tips of the wings. These are locations where the wings have the thinnest structure and might need to be both stronger and lighter—an example, perhaps, of nature using math to fortify itself.

“We were very happy to see these results,” said Lu. “We observed the golden angle and we saw how it was being used in areas of the wings where it was most needed, while still providing the necessary biomechanical and aerodynamic functions.”

He added, “My summer intern experience at Brookhaven was a fantastic way to jump-start my university studies and my future career in research.”

By the end of the summer internship, though, Lu and Huang had yet to explain the 101-degree outlier peak. Huang shelved the project and didn’t fully revisit it until nearly two years later.

More results take shape

In the summer of 2021, Huang teamed up with Shen to attempt to continue where Lu’s research had left off.

“We already had a good story with good results, but I wanted to know if Sam could explain what Keene and I couldn’t,” said Huang.

Shen launched into the project. He started his independent study by looking at the vein angles in the dragonfly wings’ venation patterns; he was interested in more than the golden angle. He noticed there were many outliers in the vein angle patterns, and they occur at the same angles for both forewing and hindwing.

enlarge

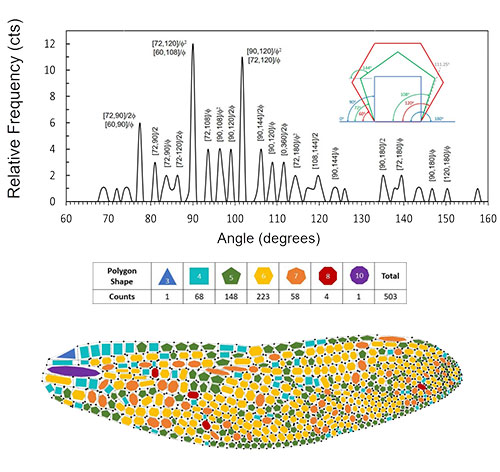
The top graph shows angle positions of the residuals from the Gaussian-peak fitting for the dragonfly forewing. The center table shows the relative occurrence frequencies of the predicted preferred angles given by golden-rule partitions of the intervals between regular angle pairs in perfectly shaped quadrilateral, pentagon, and hexagon venation cells. The bottom image depicts polygon shapes in the venation pattern of a dragonfly wing. It shows that hexagons, pentagons, and quadrilaterals are the most popular shapes in the pattern.

Driven by curiosity, Shen researched the literature and recognized that many of the golden angle appearances in published studies happen in natural examples that are not subject to physical constraints, such as the growth of new leaves on plants. But the dragonfly wings are different; their vein patterns are bound by the wing boundary. This additional constraint may make a big difference in how the golden ratio is applied to dragonfly wing patterns.

Inspired by this idea and a paper on golden-angle partition rules on plant leaves, Shen created a new model to explain the venation patterns in dragonfly wings. He first observed that the most numerous shapes in the wing patterns were irregularly shaped hexagons, pentagons, and quadrilaterals. Since each shape comes with a set of angles—a square has four 90-degree angles, for example—this gave him a starting point.

“From what I learned in the literature, I came up with a new mathematical model to provide the analysis and interpretation on the statistically significant outliers in the vein angle histograms,” he said.

Shen’s model predicts a set of preferred intervein angles in the venation patterns using the shape angles, factoring in the golden ratio and the frequency of occurrences. He then compared the distribution of this set of angles to Lu’s distribution. The results were striking. His model’s predicted results matched remarkably well with Lu’s measured data, indicating these previously thought outliers are, in fact, the preferred intervein angles governed by the golden ratio.

“It’s really amazing how Sam’s results align so closely with Keene’s,” said Huang. “I have to credit him for his excellent research and analysis. Both he and Keene really impressed me with the way they took this project and ran with it.”

Recognizing he was clearly on the right track, Shen continued to work with his model, looking for an explanation for the 101-degree outlier—and he found it. The model predicts that some angles have a higher probability of occurrence, and this includes 101 degrees. In fact, Shen’s model explains not only the main outlier at 101 degrees, but also almost all other secondary outliers at other angles, further proving these are not outliers but rather preferred angles.

Shen said, “I am honored to be part of this team and to make a critical contribution to the work. This research made me realize that one should always cherish new thinking and be persistent to tackle obstacles.”

He continued, “Contributing to such a scientific paper is an incredible experience for my future career. I’d like to thank Dr. Huang for his invitation to join this project as well as the High School Research Program, which allowed me to pursue research at Brookhaven.”

“This is another amazing example of how beauty, math, and biomechanics are brought together in nature,” said Miller. “In their work, Xiaojing made an observation from the beauty of dragonfly wings and Keene and Sam used mathematics principles to describe the geometrical patterns to explain how they optimize the wing’s biomechanics for flight.”

Aleida Perez, the Office of Educational Programs’ Manager of University Relations and DOE Programs, added, “The HSRP provides students like Sam and Keene with an authentic experience and the opportunity to be active contributors to exciting and impactful scientific research. These kinds of programs support their development of scientific skills and help build their collaborative future educational and professional network. Keene also participated in the Science Undergraduate Laboratory Internships (SULI) program for the 2023 summer term, showing how HSRP is an effective pathway to the DOE internship programs.”

Brookhaven National Laboratory is supported by the Office of Science of the U.S. Department of Energy. The Office of Science is the single largest supporter of basic research in the physical sciences in the United States and is working to address some of the most pressing challenges of our time. For more information, visit science.energy.gov.

Follow @BrookhavenLab on social media. Find us on Instagram, LinkedIn, Twitter, and Facebook.