Electron Spectroscopy Group
Research
This program undertakes the study of the basic electronic excitations of topological insulators and strongly-correlated electron systems with the goal of understanding the complex metallic character at high temperature and the novel ground states that emerge at low temperatures. To this end, angle-resolved photoemission spectroscopy (ARPES) and optical spectroscopy, complementary techniques, are used to study the properties of the low-energy excitations and associated dynamics in these systems. In concert with this, studies of the 5d irridate and osmium oxide materials (structural analogs to the cuprates) will be undertaken in order to gauge the effects of strong spin-orbit coupling as it relates to the possibility of superconductivity, topological Mott insulators and other emergent phases and phenomena.
Superconductivity, competing orders, and critical phenomena
Since their discovery over 25 years ago, the mechanism of superconductivity in the copper-oxide materials has proven elusive. The parent compounds are Mott insulators; chemical substitution results in either electron or hope doping and the evolution into a strange metal. At low dopings, static charge- and spin-stripe order develop at low temperature, competing with and frustrating the formation of a superconducting state. However, as the carrier doping increases the charge (and spin) order melts or begins to fluctuate, allowing a superconducting state to emerge at relatively high temperatures. In the normal state of the underdoped region, a peculiar feature known as the pseudogap emerges with decreasing temperature; this state was originally identified in transport and NMR measurements; later optics work on the optical conductivity perpendicular to the highly-conducting copper-oxygen planes (c axis) revealed that as the temperature is lowered the low-frequency optical conductivity is suppressed, reminiscent of a transport gap. However, this pseudogap along the c axis evolves in an almost continuous fashion with temperature with no anomalous behavior at the critical temperature (Tc). ARPES studies were able to show that while the Fermi surface in the over-doped materials was large, as the doping decreased into the pseudogap state, the Fermi surface retreated to the nodal regions. There has been a considerable debate as to the detailed nature of the Fermi surface in the nodal regions, which are discussed as either arcs or pockets. The conventional interpretation of the phase diagram considers the normal state of the underdoped materials to be a non-Fermi liquid, which is to say the correlations extend beyond simple e-e interactions. Recent work on the single layer HgBa2CuO4 +d (which displays the highest value for Tc in the class of materials that have only one copper-oxygen layer in the unit cell) shows a strong Fermi-liquid behavior in the normal-state scattering rate. On the other hand, the unusual power- law behavior of the optical conductivity in underdoped YBa2 Cu3O6+x indicates a non-Fermi liquid behavior. As the optical measurements along the c axis and numerous other studies demonstrate, the pseudogap extends into the superconducting dome in the cuprates, suggesting that for some critical doping there is a zero-temperature phase transition or quantum critical point (QCP); it has been argued that this QCP may be the key to understanding both hightemperature superconductivity and the anomalous normal-state properties in these materials. The lack of a consensus about the true nature of the pseudogap indicates that further study across a wider variety of systems is merited.
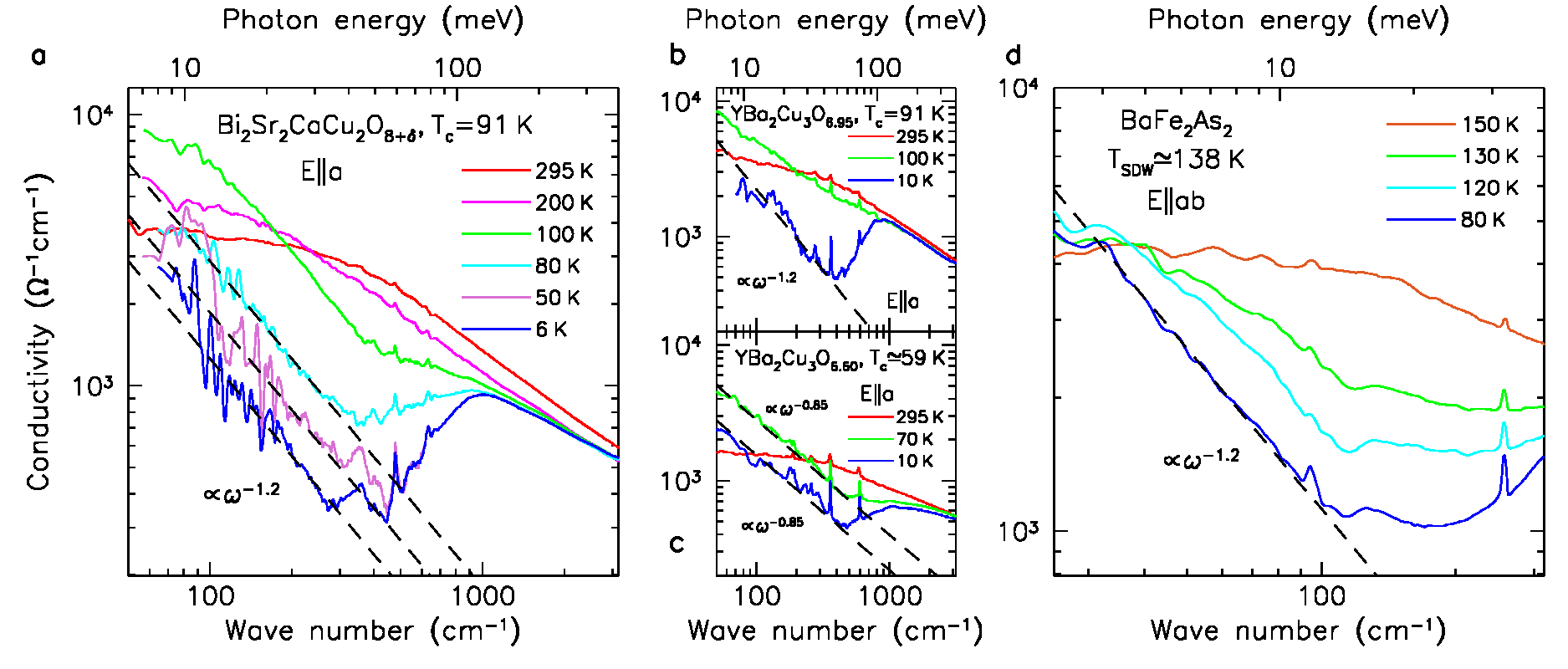
Fig. 1: (a) The temperture dependence of the optical conductivity versus wave number (photon energy) for optimally-doped BSCCO (Tc = 91 K) for light polarized along the crystallographic a axis. At low frequency just above Tc the material may be cautiously described as a Fermi liquid. For all the temperatures measured below Tc the residual conductivity from the unpaired quasiparticles follows the same non-Fermi liquid fractional power law. (b) The plot for optimally-doped YBCO6.95 (Tc =91 K), for light polarized along the a axis, illustrating the same fractional power law below Tc. (c) The plot for underdoped YBCO6.60 (Tc = 59 K), for light polarized along the a axis, illustrating an identical (non-Fermi liquid) fractional power law behavior in the a-b planes in the normal (pseudogap) and superconducting states. (d) The plot for BaFeAs2 (TSDW = 138 K), for light polarized in the a-b planes. Below TSDW a fractional power law is again observed.
In a conventional BCS superconductor, the optical conductivity is expected to be quite low for T << Tc at frequencies below twice the gap energy. In the cuprate materials there is a significant amount of low-frequency residual conductivity even for T << Tc; this is particularly true in the optimally-doped bilayer BSCCO and YBCO materials. This is due to the unusual d-wave nature of the superconducting energy gap; at temperatures well below Tc and for photon energies well below the gap maximum, the electronic dispersion in the nodal region is a vertex that is reminiscent of a Dirac-like cone. The collapse of the transport scattering rate below Tc ensures that in the far-infrared we are in the region where the frequency is much greater than the scattering rate, where the real part of the optical conductivity is expected to vary as one over the square of the frequency for both the Fermi liquid and Drude model. However, for those cuprates where the opening of a gap below Tc may be clearly observed and the residual conductivity carefully measured, the surprising non-Fermi liquid response is roughly inverse with frequency, shown for BSCCO in Fig. 1(a). Similarly, the parent materials for some of the iron-based superconductors AFe2As2 (A = Ba, Ca and Sr) undergo a spin-density-wave (SDW) transition which results in a reconstruction of the Fermi surface with Dirac-like cones in the electronic dispersion; interestingly, the low-frequency residual conductivity in the SDW state of these materials has the identical power-law behavior that was observed for the cuprate materials. The identification of an inverse (or fractional) power-law behavior in the residual optical conductivity now permits the removal of this contribution, revealing the direct transitions across the gap and allowing the nature of the electron-boson coupling to be probed. We speculate that this apparently universal behavior is related to the similar Fermi surface topology in the ground states of these materials.
Topological insulators (TI)
Topological insulators are a new class of insulators in which the bulk gap is inverted due to strong spin-orbit coupling (SOC). They represent a new state of matter, which, unlike superconductivity, does not require the breaking of any particular symmetry - TIs are distinct from other quantum states by their topology. On the interfaces of these materials with ordinary ("trivial") insulators, gapless states inevitably occur, topologically protected by time reversal symmetry. Three- dimensional (3D) TIs thus have surface states with an odd number of massless Dirac cones in which the spin of the electron is locked perpendicular to its momentum in a chiral spin-structure where electrons with opposite momenta have opposite spins. A consequence of this spin-momentum locking is that the backscattering, requiring a spin-flip process, is not allowed if a time-reversal-invariant perturbation, is present. In related topological crystalline insulators (TCI), the existence and protection of surface states is dictated by discrete point-group symmetries of the underlying lattice. The protected surface states on both TIs and TCIs offer a platform for low-dissipation transport devices and are potentially very promising for spintronics and for quantum computing applications, where spin-coherence is crucial. However, the real materials discovered thus far all show overwhelming bulk conductivity that renders the response of the topological state virtually invisible. This makes the existing TIs impractical for any application, in spite of other favorable features, such as exceptionally weak electron-phonon coupling, that would otherwise allow functionality of devices even at ambient temperatures. Therefore, the search for new and improved materials is crucial for further development and will require a very tight connection between the theory, synthesis and spectroscopic and transport studies.
The physics of TIs is expected to become even more interesting with inclusion of electronic correlations: when interacting with magnetism or superconductivity, TIs are predicted to result in extremely fascinating phenomena, ranging from induced magnetic monopoles, anomalous quantum Hall state and Majorana fermions, and are clearly worth investigating further from the theoretical and experimental perspectives. Another direction for future development is to explore materials where the strong electronic correlations are intrinsic - in transition metal oxides (TMO). Comparable correlation, band and SOC energies in 5d TMOs could result in very rich phase diagrams, with some new exotic phases and phenomena such as topological Mott insulators and Weyl semi-metals, possibly nearby some more conventional phases, such as superconductivity and various charge- and spin-ordered phases. The competing and/or cooperation of different phenomena might result in suppression or enhancement of particular properties. Promising materials include Ir pyrochlores that have been already synthesized as bulk crystals. However, thin 5d transition metal oxide (TMO) lms and hetero-structures involving topological and "trivial" magnetic and/or superconducting TMOs might offer access to a much broader variety of new phenomena than the bulk materials and will be pursued within this project.
One of the fundamental predictions for the topological surface states (TSS) is that a time-reversal symmetry breaking perturbation, such as the introduction of magnetic impurities on the surface, is expected to open a back-scattering channel and induce a gap at the Dirac point. In our previous ARPES studies, we have tested this prediction and directly compared the effects of non-magnetic and magnetic impurities on the TSS. Quite unexpectedly, those studies have indicated that there is essentially no difference between the two types of scatterers and that the topological state is remarkably insensitive to both non-magnetic and magnetic impurities in the low doping regime, where the Fermi surface (FS) is nearly circular. Instead, the scattering rates depend on the FS shape, which can be tuned by doping. We also found no evidence for an opening of a gap at the Dirac point of the TSS. The question of inelastic scattering and in particular the strength of electron-phonon coupling is also very important as electron mobilities, important for functioning of electronic devices, are usually limited at elevated temperatures by scattering on phonons. The elastic scattering imposes the ultimate limit on charge transport, inelastic scattering processes dictate the material's transport properties at finite temperatures. In particular, interactions of electrons with lattice modes are responsible for increasing resistivity with temperature in conventional metals and there is no an a priori reason why this should not happen in TIs.
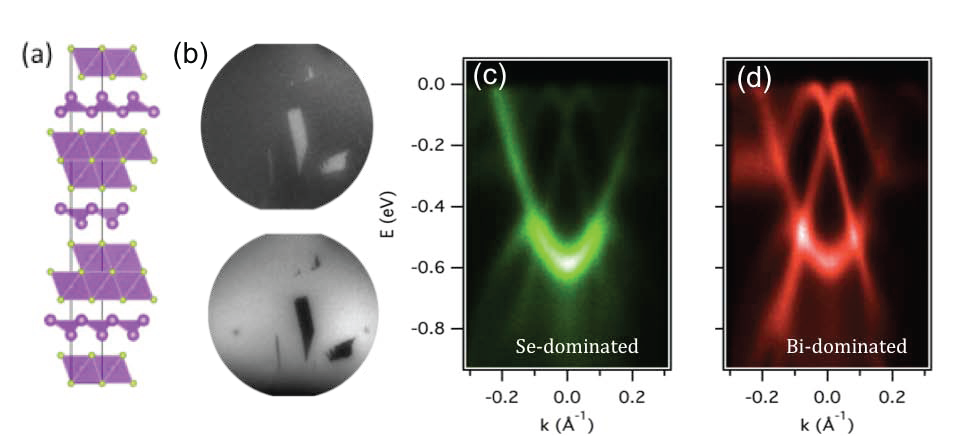
Fig. 2: Two types of topological states on Bi4Se3. (a) Crystal structure of Bi4Se3. (b) Photoemission microscopy images of Bi4Se3 surface taken at Se 3 d (up) and Bi 5d (down) core levels. Inverted contrast indicates two different terminations: Bi and Se. ARPES spectra on Se-dominated (c) and Bi-dominated (d) regions show that these two terminations have two different types of topological surface states.
Our ARPES studies from Fig. 2 show that, contrary to expectations, electrons on surfaces of these new materials are also protected from scattering on lattice vibrations and remain coherent, even at ambient temperatures. In addition, our spin-resolved ARPES (SARPES) measurements show that the states remain 100% spin-polarized at room temperature. This suggests that topological insulators could serve as a basis for wide-spread applications in room temperature electronic devices.




